http://en.wikipedia.org/wiki/Euler%27s_for...ntial_equations
Being a 2nd-order differential equation, there are two linearly independent solutions that satisfy it:
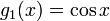

Both cos and sin are real functions in which the 2nd derivative is identical to the negative of that function. Any linear combination of solutions to a homogeneous differential equation is also a solution. Then, in general, the solution to the differential equation is


Dat er geldt dat de tweede afgeleide van cos(x) = -cos(x) en sin(x) = -sin(x) snap ik wel, maar hoe komen ze op oplossingen in de vorm van: