Ik hoor op het forum heel vaak de kreet "matrix" vallen.
nu ben ik alleen bekend met de matrix waar mensen gewoon bukken om kogels te ontwijken maar toch heb ik ook intresse om achter de wiskundige(neem ik aan) matrix te komen.
Kan iemand mij uitleggen wat je er mee kan.
en kan iemand me uitleggen hoe het werkt
En als het niet veel moeite is uitlegegn hoe ik het kan gebruiken.
Ik heb geen idee hoe ingewikkeld het is.
ps. ik kan me voorstellen dat het nogal veel werk is, dus met een goede link ben ik ook al meer dan tevreden.
Laatste berichten
-
15:28
Vraag 2009 Juli Vraag 5 5
-
12:51
positie 2
-
10:44
Schroefdraad berekening 8
-
00:15
[scheikunde] Kan chloorgas de geleiding van elektriciteit belemmeren? 9
-
21:15
Weerfrustratie 9
-
18:08
geen minkowski-ruimte toch? Doe ik dit nou fout? 15
-
23 apr
do-re-mi-fa-so vliegtuigen 7
-
23 apr
Kunnen quantum Zonnecellen 190% quantum efficiënt zijn 3
-
23 apr
De Euro Nederlandse 100 qubit computer komt eraan
-
23 apr
projectiel 8
-
23 apr
Verschil tussen deze 2 vragen 5
-
23 apr
[scheikunde] berekeningen labo vitamine c bepaling 1
-
22 apr
[wiskunde] rode en witte ballen verdelen 8
-
22 apr
Rotatie van het heelal 41
-
22 apr
Muntje opgooien 14
-
21 apr
Reactiviteit silyl enol ethers 1
-
21 apr
Criterium voor vochtretentie
-
21 apr
speciale rel. theorie 5
-
21 apr
Vogels in de stad zijn goede klussers
-
21 apr
Ervaringen met "herontdekkingen" 15
Nieuwsberichten
-
04 mar
Een nieuw soort magnetisme: altermagnetisme
-
31 okt
AI kan via stem diabetes vaststellen 11
-
21 okt
Einstein krijgt wéér gelijk 45
-
07 feb
witter dan wit 20
-
19 jun
irrigatie en de aardas
Wat doet een matrix
Forumregels
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de Huiswerkbijsluiter
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de Huiswerkbijsluiter
-
- Berichten: 222
Re: Wat doet een matrix
misschien dat je hier wat aan hebt: http://www.sosmath.com/matrix/matrix.html
De inhoudsopgave ziet er iig veelbelovend uit.
De inhoudsopgave ziet er iig veelbelovend uit.
"If you're scared to die, you'd better not be scared to live"
-
- Berichten: 294
Re: Wat doet een matrix
simpel gezegd is een matrix een element van R^(mxn), finja, daar ben je waarshcijnlijk niet veel mee (kan trouwens ook C zijn (complexe getallen ipv reele)
Een matrix is een element van bovenvermelde vectorruimte, en is eenvoudig te zien als een soort *tabel* met m rijen, n kolommen
vb 3x2 (m=3,n=2)
[1 0]
[0 5]
[7 9]
algemener:
[A11 A12 A12 ... A1n]
[A21 A22 A22 ... A2n]
[A31 A32 A32 ... A3n]
[.............................]
[.............................]
[.............................]
[Am1 Am2 Am2 ... Amn]
(... wil eventjes doorgaan, vrij evident)
met elk element Aij (op i-e rij en j-e kolom) element van R (of als je wil C)
dat is de *definitie* van een matrix.
nu wat is het nut van een matrix?
het heeft erg veel nut als je de algoritmen kent, daar is echter veeel tijd nodig om helemaal uit te leggen..
wat je bvb kan doen
je hebt een stelsel voor een bepaald probleem
ik zeg bvb
x1+3*x2+5*x3 = 12
3*x1+x2-x3 = 3
x1+6*x2-x3 = 10
(kweetniet of het steek houd, maja)
ipv bvb x3 op te lossen uit 3e vgl en dan in vullen in 2e, daaruit x2 halen en die dan in 1e vgl steken zodat je x1 vind vervolgens x2 en dan x3
kan je dit probleem erg vlug vertalen dmv Matrixvermenigvuldiging...
tkomt er op neer dat ge zegt dat dit stelsel overeenkomt met
met dus eerste twee matrices vermenigvuldigd
om dat te doen moeten eerst dimensies kloppen
een (m x n) matrix kan je vermenigvuldigen met een (n x p) matrix
het aantal kolommen van de eerste moet gelijk zijn aan het aantal rijen van de tweede.
bvb
het ij-e element van AB wordt algemeen gegeven door
sum(Aik. Bkj, k = 1..n)
dusja, voor het ij e element neem je de i-e rij van A en de j-e rij van B
wat doe je, je neemt eerste element van Ai* (Ai* is een rij, die ster slaat op 'daar moet nog wat komen dat nu nog niet gedefinieerd is') en vermenigvuldigd dat met het eerste element van B*j (terug zelfde betekenis ster) en dan doe je hetzelfde met de tweede elementen enzoverder, tot je aan n-e element van Ai* resp B*j zit. Die getalletjes sommeer je allemaal....
finja, komt er op neer dat je dmv Gaussreductie eenvoudig de oplossing kan vinden van het stelsel... kga dat nu hier ook niet uit de doeken doen, want das terug een bom schrijfwerk..
natuurlijk voor zon klein stelsel valt de pen-en-papier methode nogal mee, maar als je 100 variabelen hebt, kan je die heel makkelijk in zon stelsel gieten. ik gaf voorbeeld van vierkante matrix (m=n) maar dat kan ook algemener....
wat ook ander mogelijkheid is, is de voorstelling van een homomorfisme. Als je een vectorruimte V hebt en een vectorruimte W, dan kan je zeggen dat je met elke vector van V een vector van W associeert. Als je ervoor zorgt dat die operatie die je doet lineair is, spreek je van een lineaire transformatie. (vb. neem T de operatie, v1 en v2 element van V, en w1 en w2 element van W, lambda en mu zijn elementen van R of C =>
T is lineair als
T(lambda*v1+mu*v2)= lamda*T(v1)+mu*T(v2) en dan kan je T(v1) = w1 en zelfde met v2)
finja, om lang lang verhaal kort te maken, kan je een basis kiezen in V net zoals een in W...
je kan dan coordinaatvoorstelling maken van elke vector, en dan neem je als kolommen de coordinaatvoorstelling van de transformaties van de basisvectoren van V tov de basis van W
finja, als ge nog mee zijt. zo kunt ge bvb een populatie-evolutie bijhouden aan de hand van matrices...
andere mogelijkheden zijn bvb spiegelingen tov vlakken of projecties op vlakken of .... voor te stellen. Toepassingen zijn legio....
als je mijn cursus lineaire algebra eens wil lenen
mvg
Andy
Een matrix is een element van bovenvermelde vectorruimte, en is eenvoudig te zien als een soort *tabel* met m rijen, n kolommen
vb 3x2 (m=3,n=2)
[1 0]
[0 5]
[7 9]
algemener:
[A11 A12 A12 ... A1n]
[A21 A22 A22 ... A2n]
[A31 A32 A32 ... A3n]
[.............................]
[.............................]
[.............................]
[Am1 Am2 Am2 ... Amn]
(... wil eventjes doorgaan, vrij evident)
met elk element Aij (op i-e rij en j-e kolom) element van R (of als je wil C)
dat is de *definitie* van een matrix.
nu wat is het nut van een matrix?
het heeft erg veel nut als je de algoritmen kent, daar is echter veeel tijd nodig om helemaal uit te leggen..
wat je bvb kan doen
je hebt een stelsel voor een bepaald probleem
ik zeg bvb
x1+3*x2+5*x3 = 12
3*x1+x2-x3 = 3
x1+6*x2-x3 = 10
(kweetniet of het steek houd, maja)
ipv bvb x3 op te lossen uit 3e vgl en dan in vullen in 2e, daaruit x2 halen en die dan in 1e vgl steken zodat je x1 vind vervolgens x2 en dan x3
kan je dit probleem erg vlug vertalen dmv Matrixvermenigvuldiging...
tkomt er op neer dat ge zegt dat dit stelsel overeenkomt met
Code: Selecteer alles
[1 3 5 ] [x1] [12]
[3 1 -1] [x2] = [3 ]
[1 6 -1] [x3] [10]om dat te doen moeten eerst dimensies kloppen
een (m x n) matrix kan je vermenigvuldigen met een (n x p) matrix
het aantal kolommen van de eerste moet gelijk zijn aan het aantal rijen van de tweede.
bvb
het ij-e element van AB wordt algemeen gegeven door
sum(Aik. Bkj, k = 1..n)
dusja, voor het ij e element neem je de i-e rij van A en de j-e rij van B
wat doe je, je neemt eerste element van Ai* (Ai* is een rij, die ster slaat op 'daar moet nog wat komen dat nu nog niet gedefinieerd is') en vermenigvuldigd dat met het eerste element van B*j (terug zelfde betekenis ster) en dan doe je hetzelfde met de tweede elementen enzoverder, tot je aan n-e element van Ai* resp B*j zit. Die getalletjes sommeer je allemaal....
finja, komt er op neer dat je dmv Gaussreductie eenvoudig de oplossing kan vinden van het stelsel... kga dat nu hier ook niet uit de doeken doen, want das terug een bom schrijfwerk..
natuurlijk voor zon klein stelsel valt de pen-en-papier methode nogal mee, maar als je 100 variabelen hebt, kan je die heel makkelijk in zon stelsel gieten. ik gaf voorbeeld van vierkante matrix (m=n) maar dat kan ook algemener....
wat ook ander mogelijkheid is, is de voorstelling van een homomorfisme. Als je een vectorruimte V hebt en een vectorruimte W, dan kan je zeggen dat je met elke vector van V een vector van W associeert. Als je ervoor zorgt dat die operatie die je doet lineair is, spreek je van een lineaire transformatie. (vb. neem T de operatie, v1 en v2 element van V, en w1 en w2 element van W, lambda en mu zijn elementen van R of C =>
T is lineair als
T(lambda*v1+mu*v2)= lamda*T(v1)+mu*T(v2) en dan kan je T(v1) = w1 en zelfde met v2)
finja, om lang lang verhaal kort te maken, kan je een basis kiezen in V net zoals een in W...
je kan dan coordinaatvoorstelling maken van elke vector, en dan neem je als kolommen de coordinaatvoorstelling van de transformaties van de basisvectoren van V tov de basis van W
finja, als ge nog mee zijt. zo kunt ge bvb een populatie-evolutie bijhouden aan de hand van matrices...
andere mogelijkheden zijn bvb spiegelingen tov vlakken of projecties op vlakken of .... voor te stellen. Toepassingen zijn legio....
als je mijn cursus lineaire algebra eens wil lenen
mvg
Andy
-
- Berichten: 1.460
Re: Wat doet een matrix
Het is natuurlijk een leuk verhaal van Andy, ik hou het toch liever bij een link 
http://nl.wikipedia.org/wiki/Matrix_%28wiskunde%29
Maar wil je meer weten van matrices? Spijker je Duits een beetje bij of laat het online vertalen.
http://de.wikipedia.org/wiki/Matrix_%28Mathematik%29
http://nl.wikipedia.org/wiki/Matrix_%28wiskunde%29
Maar wil je meer weten van matrices? Spijker je Duits een beetje bij of laat het online vertalen.
http://de.wikipedia.org/wiki/Matrix_%28Mathematik%29
<i>Iets heel precies uitleggen roept meestal extra vragen op</i>
-
- Berichten: 294
Re: Wat doet een matrix
(net examen lineaire algebra achter de rug, kmoest er dus toch wel iets zinnigs over kunne vertellen e.... kan mij wel voorstellen dat nogal onduidelijk geschreven is, tklopt wel maar waarsch niet heel duidelijk voor een leek als het over matrices gaat...)
-
- Berichten: 1.750
Re: Wat doet een matrix
ik ben begonnen met de link van "friendly ghost"
ik denk deze te snappen:
je moet dus de de middelste(de rechtse van voor het = teken)
vermenigvuldigen met de linkse. dat doe je door de bovenste van de misselste te vermenigvuldigen met de linkste rij van de linkste, en de middelste van de middelste matrix doe je met de middelste rij van de linkse. snappen jullie mijn uitleg??
zit ik goed, of is de gedachten gang iets wat toevallig klopt.
maarwaarom geeft de volgende matrix vermenugvuldiging de volgende uitkomst:
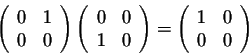
waarom doen ze de enecoordinaat maal de andere coordinaat?
ik denk deze te snappen:
je moet dus de de middelste(de rechtse van voor het = teken)
vermenigvuldigen met de linkse. dat doe je door de bovenste van de misselste te vermenigvuldigen met de linkste rij van de linkste, en de middelste van de middelste matrix doe je met de middelste rij van de linkse. snappen jullie mijn uitleg??
zit ik goed, of is de gedachten gang iets wat toevallig klopt.
maarwaarom geeft de volgende matrix vermenugvuldiging de volgende uitkomst:
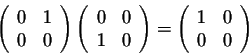
waarom doen ze de enecoordinaat maal de andere coordinaat?
-
- Berichten: 24.578
Re: Wat doet een matrix
Het voorbeeld dat je daar aanhaalt en uitwerkt klopt niet, de dimensies van de matrices komen niet overeen.
Je probeert een 2x3 matrix te vermenivuldigen met een 3x1 en dat kan niet, wél als die 2e een 3x2 geweest was...
Als je een basis Engels beheerst ben je hier wel wat mee, "Ordinary Matrix Product"
http://en.wikipedia.org/wiki/Matrix_multip..._matrix_product
Je probeert een 2x3 matrix te vermenivuldigen met een 3x1 en dat kan niet, wél als die 2e een 3x2 geweest was...
Als je een basis Engels beheerst ben je hier wel wat mee, "Ordinary Matrix Product"
http://en.wikipedia.org/wiki/Matrix_multip..._matrix_product
-
- Berichten: 23
Re: Wat doet een matrix
Dat klopt niet
m*p X p*n = m*n
die m mag verschillend zijn van die n!
(met voor de * het aantal rijen, na de * het aantal kolommen)
mvg
m*p X p*n = m*n
die m mag verschillend zijn van die n!
(met voor de * het aantal rijen, na de * het aantal kolommen)
mvg
-
- Berichten: 24.578
Re: Wat doet een matrix
Ja, dat bedoelde ik eigenlijk - wou dus 2x2 zeggen, maar ik kan het niet meer aanpassen
Bedankt voor de correctie hoedanook, het is inderdaad de # kolommen van de eerste dat gelijk moet zijn aan het # rijen van de tweede.
Voor Antoon is het misschien interessant op te merken dat vermenigvuldiging van matrices, integenstelling tot de intuïtie van velen, in het algemeen níet commutatief is. A*B is dus in het algemeen verschillend van B*A, gesteld uiteraard dat ze bestaan (i.e. dat de dimensies kloppen met de bovenstaande voorwaarde)
Bedankt voor de correctie hoedanook, het is inderdaad de # kolommen van de eerste dat gelijk moet zijn aan het # rijen van de tweede.
Voor Antoon is het misschien interessant op te merken dat vermenigvuldiging van matrices, integenstelling tot de intuïtie van velen, in het algemeen níet commutatief is. A*B is dus in het algemeen verschillend van B*A, gesteld uiteraard dat ze bestaan (i.e. dat de dimensies kloppen met de bovenstaande voorwaarde)
-
- Berichten: 1.750
Re: Wat doet een matrix
dit wou ik even zien:
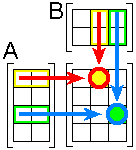
nu snap ik die vermenigvuldigingen en kan ik door met het volgende
nu snap ik die vermenigvuldigingen en kan ik door met het volgende
