Hey,
Ik ben nu al een tijdje bezig met onderstaande som, maar kom geen stap verder.
∫1/(SQRT(4-64(x)^2))dx
Wie kan mij hierbij helpen, alvast bedankt.
Laatste berichten
-
08:29
Programmeren met vectoren 5
-
23:12
speciale rel. theorie 10
-
22:57
Straatklok loopt 5 minuten voor 11
-
22:57
wig 6
-
22:36
Gravity and gravitation 4
-
22:24
[scheikunde] vraag Chemie - wat is de oplossing? 10
-
19:47
Bruine vlekken op treinaanwijzerbord 10
-
19:44
Vogels in de stad zijn goede klussers 2
-
19:12
Rood laserlicht 3
-
17:30
Herleiden afmetingen vanaf een foto 21
-
16:34
[wiskunde] Prijs Product per KG; Alternatief Inzicht 3
-
13:57
do-re-mi-fa-so vliegtuigen 9
-
13:16
geen minkowski-ruimte toch? Doe ik dit nou fout? 17
-
13:12
[natuurkunde] kroon van koning op Syracuse 10
-
25 apr
2013 – Augustus Vraag 3 3
-
24 apr
Vraag 2009 Juli Vraag 5 5
-
24 apr
positie 2
-
24 apr
Schroefdraad berekening 8
-
24 apr
[scheikunde] Kan chloorgas de geleiding van elektriciteit belemmeren? 9
-
23 apr
Weerfrustratie 9
Nieuwsberichten
-
04 mar
Een nieuw soort magnetisme: altermagnetisme
-
31 okt
AI kan via stem diabetes vaststellen 11
-
21 okt
Einstein krijgt wéér gelijk 45
-
07 feb
witter dan wit 20
-
19 jun
irrigatie en de aardas
Onbepaalde integraal
Moderators: ArcherBarry, Fuzzwood
-
- Berichten: 7.390
Re: Onbepaalde integraal
Stap 1: 4 afzonderen
Stap 2: wat dacht je van een goniometrische substitutie?
Laat maar weten als het niet lukt!
Stap 2: wat dacht je van een goniometrische substitutie?
Laat maar weten als het niet lukt!
"C++ : Where friends have access to your private members." Gavin Russell Baker.
-
- Berichten: 16
Re: Onbepaalde integraal
stap 1: 4 afzonderen
∫1/(sqrt(4(1-16^x^2))
Stap2: ik ben niet zo thuis in goniometrische substitutie. Bedoel je het toepassen van deze formule:
∫1/(sqrt(a^2-u^2))du?
∫1/(sqrt(4(1-16^x^2))
Stap2: ik ben niet zo thuis in goniometrische substitutie. Bedoel je het toepassen van deze formule:
∫1/(sqrt(a^2-u^2))du?
-
- Berichten: 7.390
Re: Onbepaalde integraal
Substitutie: stel
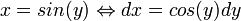. We vinden:
We gebruiken nu dat 
, en vinden:
Tenslotte terug substitueren, wetend dat 
geeft:
Herken je jouw opgave?"C++ : Where friends have access to your private members." Gavin Russell Baker.
-
- Berichten: 24.578
Re: Onbepaalde integraal
Als je hiervoor een standaardformule gezien hebt, kan je inderdaad naar deze vorm proberen te werken. Wat is a en wat is u?naomi2010 schreef:Stap2: ik ben niet zo thuis in goniometrische substitutie. Bedoel je het toepassen van deze formule:
∫1/(sqrt(a^2-u^2))du?
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
-
- Berichten: 16
Re: Onbepaalde integraal
Onderstaande stap is mij niet geheel duidelijk.
∫((1+cos(2y))/(2))dy = 1/2∫dy+1/4∫cos(2y)d(2y)
1/2∫dy is duidelijk, alleen 1/4∫cos(2y)d(2y) niet.
∫((1+cos(2y))/(2))dy = 1/2∫dy+1/4∫cos(2y)d(2y)
1/2∫dy is duidelijk, alleen 1/4∫cos(2y)d(2y) niet.
-
- Berichten: 24.578
Re: Onbepaalde integraal
Schrijf anders de substitutie u = 2y eens uit, als je dat "aanpassen achter de d" niet kent.
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
-
- Berichten: 16
Re: Onbepaalde integraal
stap 1∫((1+cos(u))/2)*dy=
stap 2 1/2∫dy+1/4∫cos(u)*(du). Helaas zie de bewerking van stap 1 naar stap 2 nog steeds niet.
stap 2 1/2∫dy+1/4∫cos(u)*(du). Helaas zie de bewerking van stap 1 naar stap 2 nog steeds niet.
-
- Berichten: 24.578
Re: Onbepaalde integraal
In de eerste stap moet nog 2y staan. Splits dan in twee en gebruik alleen voor de tweede integraal de substitutie u = 2y, wat geeft dat?
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
-
- Berichten: 16
Re: Onbepaalde integraal
stap 1∫((1+cos(2y))/2)*dy=∫1/2 + cos(2y)/2 = ∫1/2 + cos (u)/2 du
