Ik ben bezig met het ontwikkelen van een systeem dat de prestaties van een zeilboot meet en deze gebruikt om een route te plannen. Belangrijke gegevens zijn windkracht, hoek van inval van de wind en de snelheid. Je zou voor een bepaalde windkracht een pooldiagram kunnen maken waarin snelheid en invalshoek van de wind afgebeeld staan. Als je daarbij ook nog eens uitgaat van de symmetrie krijg je zoiets:
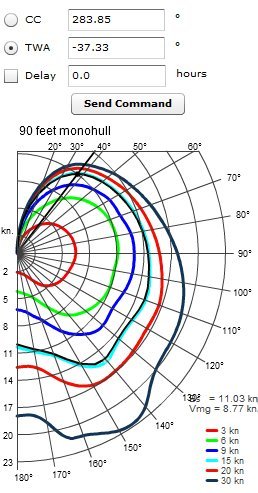
Een systeem om de data te loggen is niet het probleem, maar ik weet niet hoe ik de verwerking van de data moet aanpakken. Ik krijg heel veel datapunten waar ik per punt drie gegevens nodig heb, namelijk windkracht, invalshoek van de wind en de snelheid. Wat ik echter nodig heb bij het plannen van de route en het maken van de diagrammen is een systeem waaraan ik kan vragen: "Wat is de snelheid bij 12 knopen wind en een invalshoek van 38 graden?". Een waarde die hoogstwaarschijnlijk niet gemeten is. Ook als het punt wel gemeten is, is deze enkele meting niet precies genoeg.
Mijn probleem bestaat dus eigenlijk uit de volgende twee vragen:
- Hoe sla ik de grote hoeveelheden data efficiënt op? Moet alle data bewaard blijven, of kan ik punten samenvoegen als ik bijvoorbeeld van tevoren zeg dat 1 graad resolutie genoeg is?
- Hoe haal ik uit al deze (drie dimensionale) punten een nieuw waarde? En dan wil ik niet alleen interpoleren, maar ook een soort van gewogen gemiddelde uit meerdere waarden om eventuele uitschieters te filteren.
Alvast bedankt!