De vraag; schets het volgende, in poolcoördinaten gegeven, gebied D={
\(\theta\leq \pi\)
en \(\frac{3\pi }{4}\leq \theta\)
en \(r\leq 2\)
}.Het antwoord zoals gegeven (in zwart):
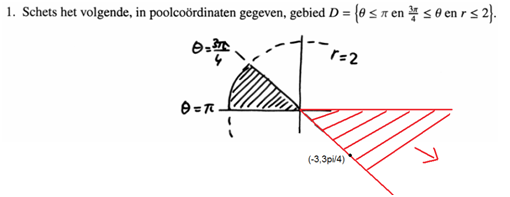
Het aangegeven domein (in zwart), is volgens mij geldig voor: D={
\(\theta\leq \pi\)
en \(\frac{3\pi }{4}\leq \theta\)
en \(0\leq r\leq 2\)
}, maar komt volgens mij niet overeen met het gegeven domein.Het domein voor D={
\(\theta\leq \pi\)
en \(\frac{3\pi }{4}\leq \theta\)
en \(r\leq 2\)
} omvat volgens mij namelijk óók het rood gemarkeerde gedeelte. Het aangegeven poolcoördinaat (-3,3pi/4), voldoet bijvoorbeeld aan de beschrijving van het gegeven domein, zover ik weet althans.Kan iemand dit bevestigen? Alvast bedankt!
