Ik moet zien te bewijzen dat 2|N aftelbaar oneindig is.
Ik kan elke even getal combineren met een natuurlijke getal zo dat
2=1, 4=2, 6=3,....
|N={1,2,3,4,5,6,.....,n} (n∈ |N)
2|N={2,4,6,8,10,12,...2n} (n∈ |N)
f: |N --> 2|N f(n)=2n,.
Ik moet bewijzen dat f bijective is dat doe ik door apart te bewijzen dat het surjectief en injectief is,
n1,n2 ∈|N
f(n1)=f(n2)
dus 2n1=2n2 dus n1=n2
dus f is injectief.
Ik weet niet hoe ik de surjectieve gedeelte moet bewijzen?
En ik weet ook niet hoe ik uiteindelijk kan stellen dat 2
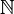aftelbaar oneindig is nadat bewezen is dat f bijective is.Bedankt! (Ik ben niet zo goed in het opstellen van bewijzen op een goede manier, want ik ben net begonnen met het leren op te stellen van bewijzen)
.