De EPR-paradox
De EPR-paradox komt eigenlijk neer op de vraag of er toeval is in het heelal. Volgens de kwantumtheorie wel, daar gebeuren dingen die enkel van het toeval afhangen. 3 wetenschappers waren het daar echter niet mee eens: Einstein, Podolsky en Rosen. Daarom bedachten ze een paradox die aantoonde dat het heelal echt niet van het toeval kon afhangen. "Als het heelal echt toevallig is", zo zeiden ze, "dan komen wij de EPR-paradox uit. De EPR-paradox is echter te raar om los te lopen, dus kan het heelal niet van toeval afhangen." Of zoals Einstein het zei met zijn beroemde woorden: "God dobbelt niet".
Om de EPR-paradox helemaal uit te leggen is echter moeilijk, ik snap het zelf niet helemaal, denk ik. Echter, de fysicus Bell heeft een heel simpele variant uitgedacht die eenvoudig was na te meten in een experiment. Dat experiment is echt eenvoudig te begrijpen, en is het experiment dat in het volgende hoofdstuk staat uitgelegd. Het is het experiment dat aantoont dat God waarschijnlijk wél dobbelt!
Het experiment van Bell
Het experiment kan op 2 manieren uitgelegd worden:
1) Je kunt het volledige experiment begrijpen zonder iets van kwantummechanica af te weten. Je moet dan enkel vertrouwen dat de meetresultaten die ik je vertel ook echt kloppen. Het experiment zelf kun je helaas niet opstellen met huis-tuin-keukengerief. Als je alles zonder de kwantumtheorie wil lezen, dan moet je gewoon alle
OF
2) Je kunt meteen erbij lezen waarom de kwantumtheorie de metingen wel verklaart! Dan moet je mij helemaal niet op mijn woord geloven, maar is het eenvoudig te zien waarom je meet wat je meet. Je moet enkel de absolute basis kennen van kwantumtheorie en je moet ongeveer weten hoe een polarisatiefilter werkt (zoals in sommige zonnebrillen of in de 3D-brillen in de cinema). Ik herhaal die stof zelfs nog eens in het begin! Om deze versie van het verhaal te kennen, moet je enkel alle blokjes met
Korte herhaling van basis-kwantumtheorie en polarisatiefilters
De opstelling van het experiment
We hebben twee identieke dozen die kunnen meten. Iedere doos heeft een hendel met 3 standen. Voor de eenvoud noemen we die standen A,B en C. Iedere doos heeft ook een aansluiting voor een bron aan de ene kant, en aan de andere kant een buzzer.
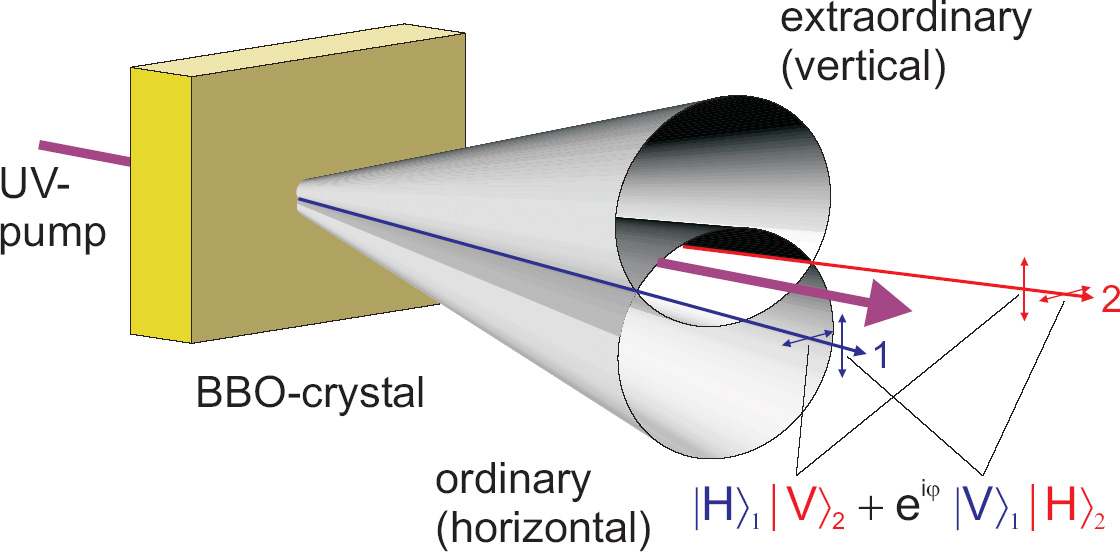
Bon, nu komt er een superslimme geleerde binnen, en die geeft ons een funky doos die hij een BBO noemt. De doos bevat 2 aansluitingen, een linker- en een rechteraansluiting. De geleerde vertelt ons dat die uitgangen bronnen zijn die we op onze andere meetdozen kunnen aansluiten. Hij vertelt ons ook dat er elke seconde een kort signaal uit de bronnen komt. Hij zegt ons tenslotte dat we niet meer hoeven te weten over hoe de doos werkt.
We doen wat de geleerde zegt, en we sluiten de twee bronnen die uit de BBO-doos komen, aan op onze twee meetdozen. De ene meetdoos op de linkeraansluiting, de andere meetdoos op de rechteraansluiting.
We hebben nu dus 2 buzzers, één per meetdoos, waarvan we het gedrag kunnen observeren.
Observatie 1) De buzzers gaan niet elke seconde af, ook al wordt iedere seconde een boodschap uit de bron verstuurd.
Hoe kunnen we die observatie verklaren?
Veronderstelling 1) We kunnen veronderstellen dat ieder boodschap die uit de bronnen komt, op het moment van de meting een eigenschap heeft die bepaalt of de buzzer af zal gaan of niet. Deze veronderstelling lijkt erg triviaal, maar wordt later nog belangrijk!
We kunnen zeggen dat een boodschap dat de buzzer bij stand A doet afgaan de eigenschap a heeft, een boodschap dat de buzzer in stand B doet afgaan de eigenschap b heeft, en een boodschap dat de buzzer bij stand C doet afgaan de eigenschap c heeft. Omgekeerd, een boodschap dat niet de buzzer doet afgaan bij een bepaalde stand, heeft de respectievelijke eigenschappen a', b' en c'.
We noemen die eigenschappen de "verborgen variabelen".
Het is eigenlijk erg eenvoudig. Stel je voor dat iedere boodschap een e-mail is, en die e-mail bevat een tekst waarin staat of de buzzer bij stand A moet afgaan, of hij bij stand B moet afgaan en of hij bij stand C moet afgaan. Onze meetdozen lezen dan die tekst en laten dan de buzzers afgaan. Die tekst bevat dus de verborgen variabelen, de eigenschappen die zeggen wat onze meetdozen moeten doen. Hoe die tekst of die verborgen variabelen er uit zien doet er niet toe, we veronderstellen alleen dat ze er zijn.
In deze veronderstelling zit nog een veronderstelling verstopt. Laten we deze even expliciet maken:
Veronderstelling 2) De boodschap heeft ook een eigenschap voor de stand van de hendel die we niet hebben gemeten.
Opnieuw, dit klinkt erg triviaal. We hebben bijvoorbeeld de hendels in stand A gezet, waardoor we niet weten wat er in stand B gebeurt. Maar we hadden de hendels ook in stand B kunnen zetten, de boodschap moet dus ook iets zeggen over wat er gebeurt in stand B. Ter vergelijking: ook als we niet naar de computer kijken, heeft de computer een eigenschap die zegt of ze aan staat of uit. Of we kijken of niet maakt niets uit.
Bovenstaande veronderstelling is zo triviaal dat ze misschien wat moeilijk te snappen is, maar toch moet ze gemaakt worden.
Voor het volgende experiment plaatsen we de hendels van beide meetdozen in dezelfde stand.
Observatie 2) Als de buzzers afgaan, dan gaan ze altijd samen af als de hendels in dezelfde stand staan. Dit geldt voor zowel stand A, B als C.
Wel, een verklaring zou kunnen zijn dat de dozen gewoon met elkaar communiceren. Maar, we kunnen de dozen als we willen zo ver uit elkaar zetten, dat als ze zouden communiceren op het moment van de meting, dat ze dat sneller dan de lichtsnelheid moeten doen, en dat kan niet volgens de relativiteitstheorie. Opnieuw, dit klinkt erg triviaal. Laten we dat even expliciet maken:
Veronderstelling 3) De dozen kunnen niet met elkaar communiceren, omdat ze niet in elkaars buurt zijn.
Observatie 2) is erg snel verklaard. Blijkbaar stuurt de BBO-doos dezelfde boodschap in beide richtingen uit. Als de linkerboodschap a is, moet de rechterboodschap dat ook zijn. Hetzelfde geldt voor b en c. De linkerbron en de rechterbron van de BBO-doos zijn dus hetzelfde.
Maar nu, wat gebeurt er als we de twee dozen op een verschillende stand zetten? Wel, we hebben 6 mogelijke combinaties: (A en B) bijvoorbeeld, of (A en C), of (B en C), of (B en A), of (C en A), of (C en B). We voeren ieder van die 6 combinaties uit.
Observatie 3) Als de hendels verschillend staan, dan heeft de rechterbuzzer exact 25% kans om hetzelfde te doen als de linkerbuzzer. Met andere woorden, 75% van de tijd gaat er 1 van de buzzers af.
OK, geen probleem zou je denken. Je bent echter verkeerd, ook al is het niet meteen duidelijk dat dit raar is. Die 25% die we meten, is namelijk veel te weinig. Maar geen probleem als je het niet meteen ziet, de grootste wetenschappers hebben dit ook tientallen jaren niet gezien. Het zou zelfs erg uitzonderlijk zijn als je meteen kunt zien waarom die 25% te weinig is.
Waarom is die 25% raar?
Nu even een tabelletje, waarmee we alle mogelijke soorten boodschappen die we met onze meetdozen kunnen onderscheiden op een rij zetten. We kunnen de hendel op 3 standen zetten, en op iedere stand hebben we 2 mogelijke uitkomsten (a of a', b of b', c of c'). In totaal geeft dat 8 verschillende boodschappen die we kunnen onderscheiden. Nu vragen we ons af wat er bij iedere soort boodschap gebeurt, als de hendel op onze meetdozen verschillend staat.
Ik voer nog even een notatie in. Als [A,B]=1, dan wil dit zeggen dat allebei de buzzers afgingen als de linkerhendel op A stond, en de rechterhendel op B, of dat geen van beide buzzers afgingen. Met andere woorden:
als [A,B]=1, dan reageren beide buzzers op dezelfde manier,
als [A,B]=0, dan reageren beide buzzers op een verschillende manier.
Die notatie is korter en maakt de tabel eenvoudiger.
| boodschap | [A,B] | [A,C] | [B,A] | [B,C] | [C,A] | [C,B] |
| a-b-c | 1 | 1 | 1 | 1 | 1 | 1 |
| a-b-c' | 1 | 0 | 1 | 0 | 0 | 0 |
| a-b'-c | 0 | 1 | 0 | 0 | 1 | 0 |
| a-b'-c' | 0 | 0 | 0 | 1 | 0 | 1 |
| a'-b-c | 0 | 0 | 0 | 1 | 0 | 1 |
| a'-b-c' | 0 | 1 | 0 | 0 | 1 | 0 |
| a'-b'-c | 1 | 0 | 1 | 0 | 0 | 0 |
| a'-b'-c' | 1 | 1 | 1 | 1 | 1 | 1 |
Tot zover mee? Als je bovenstaande tabel niet begrijpt, best even herbekijken tot je hem zelf kunt uitrekenen.
Aan deze tabel voegen we nog een kolom toe, namelijk: wat is de kans dat beide buzzers hetzelfde doen, als de hendels van beide dozen in een verschillend stand staan?
Om die kans te bepalen hebben we nog een veronderstelling nodig, die opnieuw erg triviaal klinkt.
Veronderstelling 4) De positie van de hendels hangt niet af van de boodschap.
Wat wil dat zeggen: op het moment dat je de positie van de hendels kiest, weet je niet wat er in de boodschap zit. Je kunt dus volledig vrij die positie kiezen.
Met die veronderstelling erbij is de kans dat de buzzers hetzelfde doen erg eenvoudig te berekenen. Het is namelijk het gemiddelde van de 6 kolommen ervoor. In die 6 kolommen is die kans namelijk al per stand van de hendels uitgerekend.
| boodschap | [A,B] | [A,C] | [B,A] | [B,C] | [C,A] | [C,B] | kans dat beide buzzers hetzelfde doen bij dit foton |
| a-b-c | 1 | 1 | 1 | 1 | 1 | 1 | 100% |
| a-b-c' | 1 | 0 | 1 | 0 | 0 | 0 | 33.33...% |
| a-b'-c | 0 | 1 | 0 | 0 | 1 | 0 | 33.33...% |
| a-b'-c' | 0 | 0 | 0 | 1 | 0 | 1 | 33.33...% |
| a'-b-c | 0 | 0 | 0 | 1 | 0 | 1 | 33.33...% |
| a'-b-c' | 0 | 1 | 0 | 0 | 1 | 0 | 33.33...% |
| a'-b'-c | 1 | 0 | 1 | 0 | 0 | 0 | 33.33...% |
| a'-b'-c' | 1 | 1 | 1 | 1 | 1 | 1 | 100% |
Als ieder mogelijke boodschap minstens 33,33...% van de tijd de buzzers hetzelfde laat reageren, dan wil dat zeggen dat iedere mogelijke reeks van boodschappen die je kunt bedenken hetzelfde moet doen! Je kunt niet door de boodschappen slim te combineren minder uitkomen dan 33,33...%!
Conclusie 1) Bij ongelijke stand van de hendels van beide dozen, doen beide buzzers minstens 33,33...% van de tijd hetzelfde.
Er is een tegenspraak tussen conclusie 1 en observatie 3! Een inconsistentie! Minstens 1 van onze veronderstellingen van conclusie 1 kan dus niet kloppen! Maar we hebben slechts 4 veronderstellingen gemaakt, en die waren alle 4 erg triviaal.
Maar toch, 1 van de veronderstellingen is verkeerd! En dat is precies het resultaat van het Bell-experiment. Ergens is er iets mis met ons 'triviale' beeld van het universum.
De conclusie van het experiment
Algemene conclusie van deze opzet:
1) ofwel communiceren de dozen met elkaar, sneller dan het licht
2) ofwel hebben de boodschappen geen verborgen variabelen die zeggen wat er uit de meting moet komen. Het meetresultaat wordt dus ter plekke willekeurig bepaald.
3) ofwel hebben de boodschappen echt geen eigenschappen moest de meting in een andere stand staan. Eigenschappen ontstaan pas als ze gemeten worden.
4) ofwel hangt de positie van de hendels, die we vrij gekozen hebben, echt af van de boodschap die er verstuurd werd.
Minstens één van de vier zinnen is waar. Ze kunnen niet alle 4 vals zijn, ook al zegt onze intuïtie van wel.
Waarom is ons heelal dus waarschijnlijk niet gedetermineerd
Laten we in dit hoofdstukje de 4 mogelijkheden overlopen. Er kunnen meerdere mogelijkheden kloppen, maar ze kunnen niet alle 4 verkeerd zijn.
1) Beide dozen communiceren, sneller dan de lichtsnelheid
In de wetenschap zeggen we dat het principe van lokaliteit geschonden wordt. Wat houdt dat in? Dat wil zeggen dat een meetresultaat hier kan afhangen van een gebeurtenis ver weg, nog voordat die informatie hier kan zijn.
In dit experiment hebben we dit nu enkel voor de ruimte gedaan. We hebben enkel onze dozen in de ruimte gescheiden. Maar ruimte en tijd zijn eigenlijk hetzelfde en vormen een ruimtetijd. Er zijn dus ook al voorbeelden van experimenten waarbij men kan aantonen dat men meetresultaten kan laten afhangen van beslissingen die men in de toekomst gaat nemen! Dus als je denkt dat de oplossing van de tegenspraak is dat de dozen sneller dan de lichtsnelheid kunnen communiceren, dan moet je ook aanvaarden dat er in het heelal informatie naar het verleden wordt gestuurd. Tijdreizen dus.
Dus als dit je uitweg uit het experiment van Bell is dan hangt het heden niet enkel af van het verleden, maar ook van de toekomst! Maar dan is je universum in zekere zin nog altijd gedetermineerd, er zit niet echt toeval in. Je metingen op een systeem worden gewoon beïnvloedt door informatie die je misschien zelfs nooit kunt nameten. Een meting hier kan veroorzaakt worden door een gebeurtenis aan het andere eind van het universum, miljarden jaren in de toekomst.
Je moet bij deze oplossing dus er ook bij nemen dat het heelal ook door haar toekomst gedetermineerd is. (iets wat niet onder naïeve gedetermineerdheid verstaan wordt.) Je moet bovendien heel goed oppassen dat de causaliteit nooit geschonden wordt.
(Een voorbeeld van een interpretatie van de kwantummechanica die localiteit laat vallen, is de Kopenhagen interpretatie.)
2) De boodschappen hebben geen verborgen variabelen
De boodschappen hebben geen verborgen variabelen. In wetenschappelijke termen zeggen we dat het heelal niet realistisch is. Dat houdt in dat op het moment van de meting het meetresultaat zeker een willekeurige factor bevat. Voordat we de meting uitvoeren, ligt het dus nog niet vast wat er gemeten gaat worden.
Met deze uitweg is het heelal dus duidelijk niet gedetermineerd.
(Een voorbeeld van een interpretatie die deze weg volgt is Objective collapse theory.)
3) De eigenschappen bestaan helemaal niet als je ze niet meet
Dit is een lichte variant van nummer 2). In wetenschappelijke termen zeggen we dat counterfactual definiteness niet klopt. Dus als we niet naar de maan kijken, bestaat ze niet, als niemand je moeder ziet, bestaat ze niet. Als de boom valt in het bos en niemand hoort hem, dan maakt hij geen geluid.
Met deze uitweg is het heelal opnieuw gedetermineerd, maar met erg vreemde gevolgen.
(Een voorbeeld van een interpretatie die deze weg volgt, is de veelwerelden-interpretatie van de kwantummechanica.)
4) Je keuze van de posities van de hendel hing af van de boodschap, ook al kende je hem niet
Dit houdt in dat het universum één grote samenzwering is. Het heeft er voor gezorgd dat jij die hendel koos omdat het universum wist dat het meetresultaat iets anders zou zijn dan wat de kwantumtheorie voorspelt, en dus heeft het jouw beslissing beïnvloed. In wetenschappelijke termen zeggen we dat het universum supergedetermineerd is.
Met deze uitweg is het heelal opnieuw gedetermineerd, maar in dit heelal kun je niet meer aan wetenschap doen. Je kunt namelijk geen experimenten bedenken die iets zeggen over het heelal, omdat het heelal zelf een grote samenzwering is die je gedachten beïnvloedt zodat je niets origineel kunt bedenken.
Bijgevolg is deze laatste piste niet erg populair.
Is het heelal nu gedetermineerd of niet?
Wel, alle 4 de pistes hebben aanhangers. De eerste 3 wat meer, de laatste nauwelijks. Ik heb ze hier min of meer in volgorde van populariteit onder fysici geplaatst.
Eén ding is zeker, het wereldbeeld dat je totnogtoe had, kan dus niet kloppen. Als je bovenstaande experiment echt begrijpt en haar conclusies helemaal beet hebt, dan snap je waarom wetenschappers het ook wat kwijt zijn. Dit experiment doet uitspraken over dingen die vroeger enkel filosofie waren. Hoe cool is dat...
Sowieso wordt naïef determinisme uitgesloten (ook wel causaal determinisme of nomologisch determinisme genoemd). Het is het soort determinisme dat meestal gevolgd wordt door mensen die geloven dat als we alle natuurwetten kennen en alle informatie hebben, we de toekomst van het heelal kunnen voorspellen. Het experiment toont dat dat een onhoudbare positie geworden is.
Nog vreemder is, alle metingen die gedaan werden, komen volledig overeen met wat de kwantumtheorie voorspelde. Maar om het experiment te snappen heb je helemaal geen kwantumtheorie nodig.
Echter, dit is een experiment, geen theorie! Omdat je voor het experiment dan ook helemaal geen kwantumtheorie nodig hebt, zegt het experiment nog iets bijzonders:
Wat voor theorie we ooit zullen bedenken over ons heelal, sowieso moet het bijzonder rare dingen doen op één van de vier voorgaande punten. Het universum kan volgens ons dozen-experiment niet lokaal-realistisch zijn.
Als je meer wil weten, dan raad ik het boek Teleportatie van Anton Zeilinger warm aan. Deze tekst is een korte samenvatting van dat boek.