Ik heb de opdracht gekregen om een zelfstudie te doen over numerieke integratie.
Ik zou graag een aantal vragen willen stellen, waarop ik nog geen antwoord heb gevonden.
Ik heb een integraal opgelost met de methode van intervalmiddens. Ik heb stap voor stap de uitleg in mijn bundel doorgenomen, maar mijn uiteindelijke resultaat komt niet overeen met het resultaat dat ik uitkom als ik de integraal ingeef in mijn rekenmachine.
Ik heb de oefening al een paar keer bekeken, maar ik vind niet wat ik fout heb gedaan.
Bij de trapeziumregel en de regel van Simpson heb ik niet zo goed door welke grenzen ik moet gebruiken om de deelintervallen op te lossen.
Zou iemand me kunnen helpen met deze problemen ?
In bijlage de opgave.
Bedankt !
Laatste berichten
-
15:12
Herleiden afmetingen vanaf een foto 18
-
13:27
Stank rotte eieren uit de warmwaterboiler 11
-
12:44
Nut warmtepomp 18
-
12:09
Airco bevriezings kans berekenen. 17
-
08:37
Ervaringen met "herontdekkingen" 13
-
18:53
Ik wil studeren via afstandsonderwijs, kennen jullie Tech?
-
18:09
Rotatie van het heelal 32
-
18 apr
hall effect in vloeistof gebruiken als stromingssensor 6
-
18 apr
Gezocht: de/een naam voor een getallenrij met een cauchyrij als partieelsommenrij
-
18 apr
Casus uit de praktijk: positief test THC 18
-
17 apr
speciale rel. theorie 4
-
17 apr
Vreemde stank in huis 11
-
17 apr
3 vragen over mijn rooskleurige r.berekening H2netGekoppeldeHBrflowbatterij.
-
17 apr
Interpretatie reactie-energie 3
-
17 apr
Logistic equation (Pierre Verhulst,Belgian Mathematician) 5
-
16 apr
vB 9
-
15 apr
Kunnen quantum Zonnecellen 190% quantum efficiënt zijn 1
-
15 apr
Python: sockets sluiten 4
-
14 apr
Een eenvoudige logische redenering waarom tijd niet kan bestaan 'daarbuiten' 6
-
14 apr
Hoe kun je op quantumwijze getallen vinden in een rij die kleiner zijn dan getal k 3
Nieuwsberichten
-
04 mar
Een nieuw soort magnetisme: altermagnetisme
-
31 okt
AI kan via stem diabetes vaststellen 11
-
21 okt
Einstein krijgt wéér gelijk 45
-
07 feb
witter dan wit 20
-
19 jun
irrigatie en de aardas
[wiskunde] Numerieke integratie
Moderators: ArcherBarry, Fuzzwood
-
- Berichten: 26
Numerieke integratie
- Bijlagen
-
- numerieke integratie.jpg (151.51 KiB) 676 keer bekeken
-
- Berichten: 26
Re: Numerieke integratie
Hier één van mijn oplossingen
- Bijlagen
-
- methode van intervalmiddens.jpg (199.87 KiB) 694 keer bekeken
-
- Berichten: 1.264
Re: Numerieke integratie
Je f(x_i)'s kloppen niet.
Bijvoorbeeld
Weet je wat die f(x_i)'s zijn?
Bijvoorbeeld
\(e^{\frac{-0,125^2}{2}}\)
is niet gelijk aan 0,24805 maar is gelijk aan 0,9922.Weet je wat die f(x_i)'s zijn?
Je leest maar niet verder want je, je voelt het begin van wanhoop.
-
- Berichten: 26
Re: Numerieke integratie
Ik dacht dat ik bij die f(x_i)'s de integraal moest nemen met als grenzen het deelinterval dat daarbij hoort ... Ik heb dus de integraal genomen, vandaar dat ik verkeerd uitkomFlisk schreef: ↑vr 17 jan 2014, 22:19
Je f(x_i)'s kloppen niet.
Bijvoorbeeld\(e^{\frac{-0,125^2}{2}}\)is niet gelijk aan 0,24805 maar is gelijk aan 0,9922.
Weet je wat die f(x_i)'s zijn?
Is dit ook zo bij de trapeziumregel ?
-
- Berichten: 1.264
Re: Numerieke integratie
Als je van je f(x_i) de integraal neemt kom je in jouw voorbeeld 1/4 van de integraal uit, wat ook zo is bij jou. Je moet daar de functiewaarde nemen, daarom dat het ook f(x_i) noemt.
Weet je dat een integraal een oppervlakte is? Ken je het principe van Riemannintegratie?
Numeriek integreren is de integraal benaderen. De waarde zal dus niet perfect overeenkomen, maar wel in de buurt liggen. Dit doe je door je Riemanninterval een bepaalde grootte te geven (1/4 in jouw voorbeeld).
Als je dan je functiewaarden maal die lengte doet, krijg je allemaal rechthoekjes naast elkaar. Dit is de reden waarom je niet de integraal maar de functiewaarde nodig hebt.
Dit bedoel ik:
In dit voorbeeld zou i gelijk aan 14 zijn, er zijn namelijk 14 rechthoekjes.
f(x_5) is de hoogte van het 5de rechthoekje en wordt voorgesteld door die rode verticale lijn.
Stel dat deze grafiek van x=0 tot x=7 zou lopen is de lengte van een interval gelijk aan 1/2.
De totale oppervlakte van de rechthoekjes is een benadering van de werkelijke oppervlakte onder de blauwe lijn (die de functie voorstelt).
Snap je wat ik bedoel en waarom je de functiewaarde moet nemen?
Bij de trapeziumregel ga je i.p.v. rechthoekjes, trapeziums gebruiken:
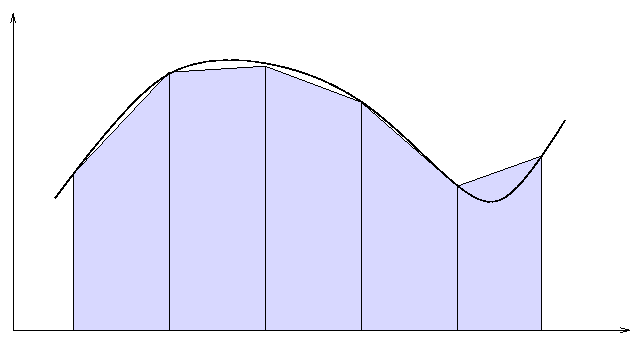
Zie je het verschil?
En ja die f(x_i) bij de trapezium zijn het ook functiewaarden die je moet gebruiken.
Weet je dat een integraal een oppervlakte is? Ken je het principe van Riemannintegratie?
Numeriek integreren is de integraal benaderen. De waarde zal dus niet perfect overeenkomen, maar wel in de buurt liggen. Dit doe je door je Riemanninterval een bepaalde grootte te geven (1/4 in jouw voorbeeld).
Als je dan je functiewaarden maal die lengte doet, krijg je allemaal rechthoekjes naast elkaar. Dit is de reden waarom je niet de integraal maar de functiewaarde nodig hebt.
Dit bedoel ik:
In dit voorbeeld zou i gelijk aan 14 zijn, er zijn namelijk 14 rechthoekjes.
f(x_5) is de hoogte van het 5de rechthoekje en wordt voorgesteld door die rode verticale lijn.
Stel dat deze grafiek van x=0 tot x=7 zou lopen is de lengte van een interval gelijk aan 1/2.
De totale oppervlakte van de rechthoekjes is een benadering van de werkelijke oppervlakte onder de blauwe lijn (die de functie voorstelt).
Snap je wat ik bedoel en waarom je de functiewaarde moet nemen?
Bij de trapeziumregel ga je i.p.v. rechthoekjes, trapeziums gebruiken:
Zie je het verschil?
En ja die f(x_i) bij de trapezium zijn het ook functiewaarden die je moet gebruiken.
Je leest maar niet verder want je, je voelt het begin van wanhoop.
-
- Berichten: 26
Re: Numerieke integratie
Ja ik snap het, dankjewel !Flisk schreef: ↑vr 17 jan 2014, 22:49
Als je daar de integraal neemt kom je in dit voorbeeld 1/4 van de integraal uit, wat ook zo is bij jou. Je moet daar de functiewaarde nemen, daarom dat het ook f(x_i) noemt.
Weet je dat een integraal een oppervlakte is? Ken je het principe van Riemannintegratie?
Numeriek integreren is de integraal benaderen. Door je Riemanninterval een bepaalde grootte te geven (1/4 in jouw voorbeeld).
Als je dan je functiewaarden maal die lengte doet, krijg je allemaal rechthoekjes naast elkaar. Dit is de reden waarom je niet de integraal maar de functiewaarde nodig hebt.
Dit bedoel ik:
In dit voorbeeld zou n gelijk aan 14 zijn, er zijn namelijk 14 rechthoekjes.
De totale oppervlakte van de rechthoekjes is een benadering van de werkelijke oppervlakte onder de blauwe lijn (die de functie voorstelt).
Snap je wat ik bedoel en waarom je de functiewaarde moet nemen?
-
- Berichten: 1.264
Re: Numerieke integratie
Graag gedaan! Het is belangrijk om dit te begrijpen, dan maak je minder snel fouten.
Ik heb mijn vorige post wat aangepast en er staat ook een voorbeeld van de trapeziumregel.
Ik heb mijn vorige post wat aangepast en er staat ook een voorbeeld van de trapeziumregel.
Je leest maar niet verder want je, je voelt het begin van wanhoop.
