Ik zit al een volle dag te puzzelen, maar kom er helaas niet uit.
Ik heb een rocket stove gebouwd, wat er ongeveer zo uit ziet:
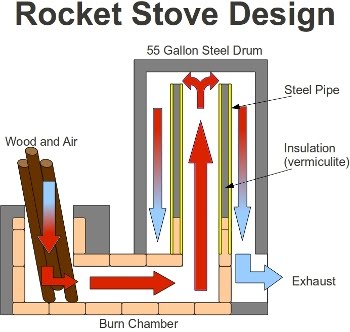
(verbluffend resultaat overigens).
De bedoeling is dat er in het midden een koperen leiding doorheen komt, die water voor een zwembad gaat verwarmen met behulp van een pomp.
Nu zag ik ergens op internet dat het erg efficiënt is als je het zo doet, dat er in het midden nog een losse cilinder komt te hangen, gevuld met water, en daar vervolgens weer je leiding doorheen laat lopen. Je conductie is met water hoger o.i.d...
Nu vraag ik me ten eerste af of dat klopt. Kan ik beter:
1. De koperen leiding simpelweg in het midden tegen de zijkant van de binnenste pijp laten lopen,
2. Een cilinder binnenin, gevuld met water, en daar de leiding doorheen laten lopen.
Nog voor de duidelijkheid wat ik bedoel, vergelijkbaar met dit:
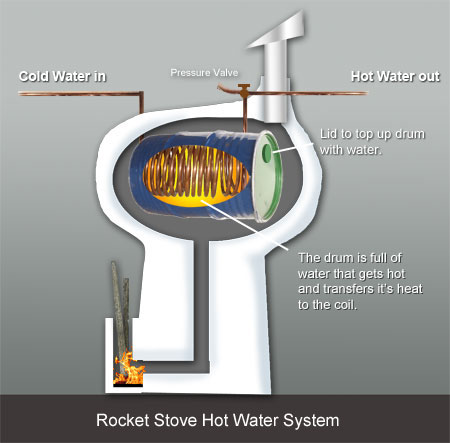
Daarnaast heb ik ook nog geprobeerd om te bepalen wat de goede verhouding is voor de lengte en diameter van het koperdraad, en de snelheid waarmee het water er doorheen moet.
Hier kwam ik vooral veel op zitten puzzelen, zonder resultaat.
Ik ben uitgegaan van een koperdraad met een lengte van 10 meter, 15mm buitendiameter en 13 mm binnendiameter. De snelheid is voor mij een raadsel.
Als eerste heb ik geprobeerd de warmtestroom te bepalen aan de hand van de volgende formule die ik op dit forum tegenkwam, maar dat lukt helaas niet, omdat ik geen idee heb hoe ik de 'h' bereken, en wat die alfa nu precies inhoudt.
Vervolgens met andere formules:
U = 1 / ( 1/h1 + Δx/λ + 1/h2 )
&
Q = U A ΔT
Met
h1 = 6000 W/m2 * K
h2 = 1000 W/m2 * K
Δx = 0,001 m
λ = 390
Kwam ik uit op U = 855
Daaruit Q afgeleid met:
U = 855
A = 2 π r h = 2*π*0,0065*10 = 0,47 m
ΔT = onbelangrijk, graadje of 40 minimaal is goed
En helaas.. ik kan het erg mooi maken, maar ik loop weer helemaal vast... Hoe ga ik zoiets bepalen? Ik heb geen idee helaas