In dit topic wil ik mogelijke ideeën om het vermoeden van Collatz te beslissen onderzoeken. Voor dat vermoeden zie:
http://nl.wikipedia.org/wiki/Vermoeden_van_Collatz
http://en.wikipedia.org/wiki/Collatz_conjecture
Laatste berichten
-
10:15
2013 – Augustus Vraag 3 3
-
09:54
Bruine vlekken op treinaanwijzerbord 6
-
23:07
Rood laserlicht 2
-
15:28
Vraag 2009 Juli Vraag 5 5
-
12:51
positie 2
-
24 apr
Schroefdraad berekening 8
-
24 apr
[scheikunde] Kan chloorgas de geleiding van elektriciteit belemmeren? 9
-
23 apr
Weerfrustratie 9
-
23 apr
geen minkowski-ruimte toch? Doe ik dit nou fout? 15
-
23 apr
do-re-mi-fa-so vliegtuigen 7
-
23 apr
Kunnen quantum Zonnecellen 190% quantum efficiënt zijn 3
-
23 apr
De Euro Nederlandse 100 qubit computer komt eraan
-
23 apr
projectiel 8
-
23 apr
Verschil tussen deze 2 vragen 5
-
23 apr
[scheikunde] berekeningen labo vitamine c bepaling 1
-
22 apr
[wiskunde] rode en witte ballen verdelen 8
-
22 apr
Rotatie van het heelal 41
-
22 apr
Muntje opgooien 14
-
21 apr
Reactiviteit silyl enol ethers 1
-
21 apr
Criterium voor vochtretentie
Nieuwsberichten
-
04 mar
Een nieuw soort magnetisme: altermagnetisme
-
31 okt
AI kan via stem diabetes vaststellen 11
-
21 okt
Einstein krijgt wéér gelijk 45
-
07 feb
witter dan wit 20
-
19 jun
irrigatie en de aardas
Vermoeden van Collatz
Moderators: Michel Uphoff, Jan van de Velde
-
- Berichten: 4.320
Re: Vermoeden van Collatz
Blijft een leuk probleem.
Helaas biedt de computer hier geen echte oplossing, die kan het vermoeden slechts aannemelijk maken.
Tenzij iemand aantoont dat het een eindig probleem is, zoals het kaart kleuren bleek te zijn en met de computer werd opgelost.
Helaas biedt de computer hier geen echte oplossing, die kan het vermoeden slechts aannemelijk maken.
Tenzij iemand aantoont dat het een eindig probleem is, zoals het kaart kleuren bleek te zijn en met de computer werd opgelost.
In de wiskunde zijn er geen Koninklijke wegen Majesteit.
Re: Vermoeden van Collatz
Idee 1. Als de rij getallen uiteindelijk op een cyclus met '1' uitloopt heb je een effect dat lijkt op een inschakelverschijnsel gevolgd door een aanhoudende trilling. Dat zou dan uit een Fouriertransformatie van die rij getallen (opgevat als 'signaal') moeten blijken.
Idee 2. Is er een differentievergelijking voor de rij getallen (opgevat als discreet signaal) op te stellen, waaruit je dan kunt afleiden wat er na zeer veel stapjes gebeurt?
Idee 2. Is er een differentievergelijking voor de rij getallen (opgevat als discreet signaal) op te stellen, waaruit je dan kunt afleiden wat er na zeer veel stapjes gebeurt?
-
- Berichten: 5.609
Re: Vermoeden van Collatz
Het probleem is dat de reeks zich chaotisch gedraagt, en dat het moeilijk is om te zeggen wat het cijfer honderd stappen verder gaat zijn. Dingen als een fouriertransformatie lijken me dus sterk.
What it all comes down to, is that I haven't got it all figured out just yet
And I've got one hand in my pocket and the other one is giving the peace sign
-Alanis Morisette-
And I've got one hand in my pocket and the other one is giving the peace sign
-Alanis Morisette-
Re: Vermoeden van Collatz
Is er geen formule of differentievergelijking bekend die voor gegeven beginwaarden de rij beschrijft? Zoiets moeten we dan inderdaad hebben, anders kunnen mijn twee ideeën niet worden toegepast.
Overigens lijkt mij een Laplacetransformatie achteraf handiger dan een Fouriertransformatie aangezien de rij enkel "naar rechts" loopt.
Overigens lijkt mij een Laplacetransformatie achteraf handiger dan een Fouriertransformatie aangezien de rij enkel "naar rechts" loopt.
Re: Vermoeden van Collatz
http://en.wikipedia.org/wiki/Collatz_conjecture#Iterating_on_real_or_complex_numbers
We hebben dus:
an+1 = f(an) .
Zodat:
Waarmee we een differentievergelijking voor an als functie van n gevonden hebben.
We hebben dus:
an+1 = f(an) .
Zodat:
\( a_{n+1} - a_n \, = \, \mbox{f}(a_n) - a_n \)
\( \Delta(a_n) \, = \, \mbox{f}(a_n) - a_n \,\, . \)
Waarmee we een differentievergelijking voor an als functie van n gevonden hebben.
Re: Vermoeden van Collatz
Nog even netjes uitschrijven (zie de eerdere link):
Dus:
Zodat (wegens het vorige berichtje):
Dit is een niet-lineaire differentievergelijking van de eerste orde.
De vraag is nu of we daaruit iets over het gedrag van an voor grote n kunnen afleiden...
\( \mbox{f}(z) = \frac{1}{4} . (2 + 7z - (2 + 5z) . \cos( \pi z)) \)
Dus:
\( \mbox{f}(a_n) = \frac{1}{4} . (2 + 7a_n - (2 + 5a_n) . \cos( \pi a_n)) \,\,\, . \)
Zodat (wegens het vorige berichtje):
\( \Delta(a_n) \, = \, \frac{1}{4} . (2 + 7a_n - (2 + 5a_n) . \cos( \pi a_n)) - a_n \)
\( \Delta(a_n) \, = \, \frac{1}{4} . (2 + 3a_n - (2 + 5a_n) . \cos( \pi a_n)) \,\,\, . \)
Dit is een niet-lineaire differentievergelijking van de eerste orde.
De vraag is nu of we daaruit iets over het gedrag van an voor grote n kunnen afleiden...
Re: Vermoeden van Collatz
De aangewezen aanpak lijkt mij hier de Z-transformatie:
http://nl.wikipedia.org/wiki/Z-transformatie
http://en.wikipedia.org/wiki/Z-transform
Helaas ben ik daar niet goed in thuis.
http://nl.wikipedia.org/wiki/Z-transformatie
http://en.wikipedia.org/wiki/Z-transform
Helaas ben ik daar niet goed in thuis.
-
- Berichten: 10.563
Re: Vermoeden van Collatz
Erdős stelde dat "de huidige" wiskunde niet in staat was dit vermoeden te bewijzen. Ik denk dat je ervan uit mag gaan dat Erdős op de hoogte was van differentievergelijkingen en Z-transformaties.
Cetero censeo Senseo non esse bibendum
Re: Vermoeden van Collatz
Ja Marko - ik weet dat de kans dat ik dit probleem zal kunnen oplossen miniem is. Maar ook als dat niet lukt heb ik er lol in en steek ik er een boel van op. Zo zal ik mij nu ook in die Z-transformatie gaan verdiepen. Daar staat bij mij al een boekje over in de kast, en dit is dan een mooie gelegenheid dat te lezen.
Laten we die discussies over de zin of onzin van mijn topics hier alsjeblieft niet herhalen.
Laten we die discussies over de zin of onzin van mijn topics hier alsjeblieft niet herhalen.
-
- Berichten: 10.563
Re: Vermoeden van Collatz
De kans is inderdaad miniem, maar belangrijker: je moet ervan uitgaan dat deze weg reeds is bewandeld. En dat maakt de kans 0.
Als je dan toch door wil blijven wandelen, dan lijkt het meer voor de hand te liggen om gebruik te maken van de vergelijking die daaronder staat beschreven:
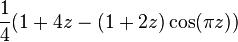
Dat maakt de differentievergelijking simpeler.
Als je dan toch door wil blijven wandelen, dan lijkt het meer voor de hand te liggen om gebruik te maken van de vergelijking die daaronder staat beschreven:
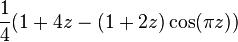
Dat maakt de differentievergelijking simpeler.
Cetero censeo Senseo non esse bibendum
Re: Vermoeden van Collatz
Als ik het goed begrijp hoort die vergelijking bij de rij bn waarvoor:
bn+1 = 1/2 . bn voor bn is even,
bn+1 = 1/2 . (3.bn + 1) voor bn is oneven.
Als an oneven is, dan is in de rij van Collatz de volgende term an+1 = 3.an + 1 + 1 even. In die rij volgt dan direct daarna: an+2 = 1/2 . an+1 . In de (ongeduldige) rij bn gebeuren die twee dingen in één stap.
Wanneer de rij bn voor alle natuurlijke beginwaarden uiteindelijk op -> 2 -> 1 -> 2 -> 1 -> 2 -> .... uitloopt, zal de corresponderende rij an voor alle natuurlijke beginwaarden op -> 4 -> 2 -> 1-> 4 -> 2 -> 1 -> 4 -> ... uitlopen. Dus kunnen we ons inderdaad tot de bestudering van de rij bn beperken.
Edit: Mijn latere bewerking (na er nog eens over te hebben nagedacht) en jouw antwoord hebben elkaar gekruist. Gelukkig komt het op het zelfde neer. Ik zal de differentievergelijking in een volgend berichtje door de simpeler versie op basis van de rij bn vervangen.
bn+1 = 1/2 . bn voor bn is even,
bn+1 = 1/2 . (3.bn + 1) voor bn is oneven.
Als an oneven is, dan is in de rij van Collatz de volgende term an+1 = 3.an + 1 + 1 even. In die rij volgt dan direct daarna: an+2 = 1/2 . an+1 . In de (ongeduldige) rij bn gebeuren die twee dingen in één stap.
Wanneer de rij bn voor alle natuurlijke beginwaarden uiteindelijk op -> 2 -> 1 -> 2 -> 1 -> 2 -> .... uitloopt, zal de corresponderende rij an voor alle natuurlijke beginwaarden op -> 4 -> 2 -> 1-> 4 -> 2 -> 1 -> 4 -> ... uitlopen. Dus kunnen we ons inderdaad tot de bestudering van de rij bn beperken.
Edit: Mijn latere bewerking (na er nog eens over te hebben nagedacht) en jouw antwoord hebben elkaar gekruist. Gelukkig komt het op het zelfde neer. Ik zal de differentievergelijking in een volgend berichtje door de simpeler versie op basis van de rij bn vervangen.
-
- Berichten: 10.563
Re: Vermoeden van Collatz
Ja, en ja. In feite wordt er een doorsteekje gemaakt, omdat de iteratie 3bn + 1 impliceert dat de volgende stap bn+1 / 2 gaat zijn. Die 2 stappen kun je ook samen nemen, en voorschrijven dat bij oneven getallen de operatie 3/2 bn+ 1/2 moet zijn.
Cetero censeo Senseo non esse bibendum
Re: Vermoeden van Collatz
Voor de rij bn hebben we:
Dus:
Zodat:
De vraag is opnieuw of we daaruit iets over het gedrag van bn voor grote n kunnen afleiden.
\( \mbox{f}(z) = \frac{1}{4} . (1 + 4z - (1 + 2z) . \cos( \pi z)) \,\,\, . \)
Dus:
\( b_{n+1} = \frac{1}{4} . (1 + 4b_n - (1 + 2b_n) . \cos( \pi b_n)) \,\,\, . \)
Zodat:
\( \Delta(b_n) = b_{n+1} - b_n \)
\( \Delta(b_n) \, = \, \frac{1}{4} . (1 + 4b_n - (1 + 2b_n) . \cos( \pi b_n)) - b_n \)
\( \Delta(b_n) \, = \, \frac{1}{4} . (1 - (1 + 2b_n) . \cos( \pi b_n)) \,\,\, . \)
De vraag is opnieuw of we daaruit iets over het gedrag van bn voor grote n kunnen afleiden.
Re: Vermoeden van Collatz
Bartjes schreef: Voor de rij bn hebben we:
\( \mbox{f}(z) = \frac{1}{4} . (1 + 4z - (1 + 2z) . \cos( \pi z)) \,\,\, . \)
Dus:
\( b_{n+1} = \frac{1}{4} . (1 + 4b_n - (1 + 2b_n) . \cos( \pi b_n)) \,\,\, . \)
Uitschrijven geeft:
\( b_{n+1} = \frac{1}{4} . (1 + 4b_n - (1 + 2b_n) . \cos( \pi b_n)) \)
\( b_{n+1} = \frac{1}{4} + b_n - \frac{(1 + 2b_n)}{4} . \cos( \pi b_n) \)
\( b_{n+1} = \frac{1}{4} + b_n - \left ( \frac{1}{4} + \frac{2b_n}{4} \right ) . \cos( \pi b_n) \)
\( b_{n+1} = \frac{1}{4} + b_n - \frac{1}{4} . \cos( \pi b_n) - \frac{1}{2} . b_n \, . \cos( \pi b_n) \,\,\,\, . \)
Waardoor:
\( \mathcal{Z}(b_{n+1}) = \mathcal{Z}(\frac{1}{4}) + \mathcal{Z}(b_n) - \mathcal{Z}(\frac{1}{4} . \cos( \pi b_n)) - \mathcal{Z}(\frac{1}{2} . b_n \, . \cos( \pi b_n)) \,\,\,\, . \)
De laatste term (de z-transformatie van het product) wordt lastig...
