Normale verdelingen

Arie Bombarie

Goede dag,

Ik ben nu met normale verdelingen bezig maar kom er nog niet helemaal uit:

Opgave 1:

Een machine die flessen vult, is ingesteld op een gemiddeld vulgewicht van 1020gram. De standaarddeviatie van het vulgewicht is onbekend. Op grond van lange series metingen is komen vast te staan dat 1,2% van alle flessen een inhoud heeft van minder dan 1000,0 gram.

Bepaal de standaarddeviatie s. Je mag hierbij aannemen dat de inhouden normaal verdeeld zijn met μ=1020 en s onbekend.

Ik neem aan dat ik Z = (x-u) / σ moet gebruiken.

Wanneer ik in het normale verdelingen tabel kijk, zie ik dat bij een kans van 0.012 een Z van 0,03 hoort.

De x is hier volgens mij 1000 gram en u = 1020 gram.

Wanneer ik de bovenstaande formule invul kom ik op een σ van 666,67 gram. Dit lijkt mij niet bepaalt logisch...

Opgave 2:

Een statisticus heeft voor zijn verzameling statistiekboeken berekend dat de dikte d van een statistiekboek kan worden beschouwd als en normaal verdeelde kansvariabele met verwachtingswaarde 2,5 cm en standaarddeviatie 0,4 cm per boek. Op zekere dag gaat hij zij boekenkast reorganiseren. Wegens tijdgebrek besluit hij stapeltjes te maken van 10 of 11 willekeurig gekozen boeken. Deze stapeltjes worden plat neergelegd op de planken van de boekenkast. De beschikbare hoogte tussen twee boekenplanken bedraagt 26 cm.

a. Hoe groot is de kans dat een stapeltje van 10 boeken niet past in de beschikbare

ruimte?

b. Hoe groot is de kans dat een stapeltje van 11 boeken wel geplaatst kan worden?

Ik neem weer aan dat ik Z = (x-u) / σ moet gebruiken.

Bij vraag a. is x volgens mij 26 cm en u = (2,5 · 10) = 25 cm

Alleen wat voor standaardafwijking moet ik hier invullen, blijft deze nu nog steeds 2,5 cm? Of wordt deze groter omdat er nu 10 boeken worden gepakt. (Is dit dan 10 · 0,4?)

Ik ben uitgegaan van een standaardafwijking van 0,4 ik krijg dan:

Een Z van: 2,5 waarbij een kans van 0,4938 hoort. Hierbij tel ik nog 0,5 op (voor alle kansen dat die kleiner dan 25 is) en kom ik uit op 0,9938

Bij vraag b. blijft de x volgens mij 26 cm en u = (2,5 · 11) = 26 cm

Bij deze vraag hetzelfde, wat moet ik hier als standaardafwijking nemen?

Ik ben uitgegaan van een standaardafwijking van 0,4 ik krijg dan:

Een Z van: -3,75 waarbij een kans van 0,4999 hoort. Hier doe ik 0,5 - 0,4999 = 1 · 10^-4

Alvast bedankt!

oscar2

Beste Arie,

Opgave 1) Bij p = 0.012 vind ik Z = 2,26. Verder lijkt je oplossing helemaal correct.

Opgave 2) mu = 2.5*10 en sigma = 0.4*10^0.5 = 1,26

2a) voor Z=2,5 vind ik P(x<Z)= 0,9938. Je moet toch eens even goed kijken naar je verdeling.

Dat is dus de kans dat de stapel past. De kans dat de stapel niet past is dus gewoon 1-0,9938

2b) zal met dit alles ook wel lukken.

Werk ze. Oscar

Arie Bombarie

Bedankt voor je antwoord!

Alleen "mijn" normale verdelingen tabel ziet er dan toch anders uit, of ik kijk niet goed...

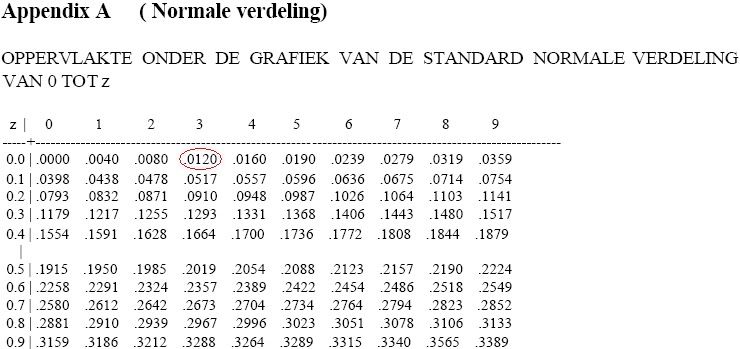
Afbeelding

Bij opgave 2:

sigma = 0.4*10^0.5

Is dit een formule? Waarin in dit geval 0,4 de standaardafwijking van in dit geval 1 boek is, de 10 van het totale aantal? En ^0,5 een soort van constante?

oscar2

Beste Arie,

1) Ja, nou zie ik het. Jij hebt een tabel van P(0 < X < z). De gevallen dat X onder het gemiddelde zit zitten er niet bij. In 2a had je daar al rekening mee gehouden. Dat betekent dat je moet zoeken naar de z met p = 0,5-0,012. Dan komen we vast op dezeflde z uit.

2) Met 10^0.5 bedoel ik 10 tot de macht 0.5 oftewel de wortel van 10. Ik heb nog niet uitgezocht hoe ik de formule krijg. 2a) is dus verder prima. Behalve dat je wel 1 - de kans moet nemen.

Eens even kijken of het nu verder lukt. Groet. Oscar

Arie Bombarie

Nogmaals bedankt voor je antwoord

.

Bij vraag 1 krijg ik nu:

P = (0,5 - 0,012) = 0,0488

In het tabel vind ik dan een waarde van Z = 2,26

Dan krijg ik:

2,26 = (1000-1020) / σ => σ = 8,850

Bij vraag 2:

a: Z = (26-25) / 0,4 = 2,5

Bij deze Z hoort een P van 0,4938

Dan doe ik: 1 - (0,5 + 0,4938) = 0,0062

b: Z = (26-27,5) / 0,4 = -3,75

Bij deze Z hoort een P van 0,4999

P = 1 - (0,4999 + 0,5) = 1 · 10^-4

Klopt het zo?

oscar2

Beste Arie,

Opgave 1) lijkt me helemaal goed zo.

Opgave 2) niet want sigma is niet 0.4. Ik heb in mijn eerste antwoord wel Z= 2,5 gebruikt om andere problemen te illustreren. Maar met de juiste waarde voor sigma is Z veel kleiner dan 2,5.

Groet. Oscar

Arie Bombarie

Dus:

2a:

(26-25)/(0,4

10) = 0,79

=> P = 0,2852

Dus P = 1 - (0,5 + 0,2852) = 0,2148

En 2b:

(26-27,5) / (0,4

11) = -1,13

=> P = 0,3708

Dus P = 1 - (0,3708 + 0,5) = 0,1292

Zo?

Wetenschapsforum

Laatste berichten

Nieuwsberichten

Normale verdelingen

Normale verdelingen

Re: Normale verdelingen

Re: Normale verdelingen

Re: Normale verdelingen

Re: Normale verdelingen

Re: Normale verdelingen

Re: Normale verdelingen