Pagina 1 van 1
Vraag over toepassing van de wet van amp
Geplaatst: vr 01 jun 2007, 00:17
door Handsome Hermit
De wet van Ampère zegt:
\( ${\displaystyle \int \vec B \cdot d \vec s}$ = \mu_0 I\)
met I de ingesloten stroom en waarbij de integraal een een lijnintegraal is. Als ik nu echter voor een torus waar het magnetische veld in de torus (dus in de ring) gelijk is aan
\(\frac{\mu_0 N I}{2 \pi r}\)
(Bron:
http://hyperphysics.phy-astr.gsu.edu/hbase...c/solenoid.html ) mag ik dan zeggen dat een lus binnen in de ring (waar er op de tekening dus enkel lucht zit) geen lading omsluit en dat dus
\( ${\displaystyle \vec B }$ \)
gelijk is aan 0?
Ik zou denken van niet omdat ik dan immers in de torus dan ook een lus kan maken om daaruit te besluiten dat het magnetische veld gelijk is 0, wat het eerste dus duidelijk tegenspreekt.
Eeuwige dank bij voorbaat.
Re: Vraag over toepassing van de wet van amp
Geplaatst: vr 01 jun 2007, 01:30
door eendavid
Je moet duidelijk onderscheid maken tussen:
- de integraal van de magnetische veld is 0
- het magnetische veld is 0
Integreer bijvoorbeeld de vector [0,0,1] eens langs een willekeurige cirkel.
Het is enkel zodra je bepaalde symmetrieën kan gebruiken, waardoor je oa op voorhand de richting van het veld kent, dat de integraalwet van Ampere tot een oplossing van het probleem kan leiden.
Maw: de integraal van het magnetische veld over een lus die binnen de spoel blijft is 0, maar het magnetisch veld niet.
Re: Vraag over toepassing van de wet van amp
Geplaatst: vr 01 jun 2007, 01:50
door Handsome Hermit
Ok, maar klopt het dan voor de toroïde dat het magnetische veld binnen in de torus-ring gelijk is aan nul omdat ik 1) weet dat de netto-omsloten stroom 0 is, 2) weet dat de lijnintegraal niet opheft omdat ik als pad voor de lijnintegraal een cirkel neem die kloksgewijs wordt doorlopen.
Situatie:
hier (deze link moest eigenlijk ook bij vorige staan.)
Re: Vraag over toepassing van de wet van amp
Geplaatst: vr 01 jun 2007, 15:07
door aadkr
Alleen in de torus zelf is de B gelijk aan de formule die je zelf gaf.
Als de grote straal van de torus veel groter is dan de kleine straal, dan mag je zeggen dat de B overal even groot is ( binnen de torus).
Buiten de torus is de B nul.
Als je de kringintegraal neemt langs een circel die geheel binnen de torus ligt, dan komt daar nul uit. Maar dat wil niet zeggen dat de B dan nul is binnen de torus.
Re: Vraag over toepassing van de wet van amp
Geplaatst: do 07 jun 2007, 10:23
door Kamarkone
En waarom is die kringintegraal van een cirkel binnenin dan gelijk aan 0 ?
Re: Vraag over toepassing van de wet van amp
Geplaatst: do 07 jun 2007, 22:12
door aadkr
De kringintegraal van de magnetische inductie genomen langs een circel binnen de torus =0
Waarom is dit?
Bekijk het oppervlak wat door de circel begrensd wordt. Gaat door dit oppervlak een elektrische stroom? Nee . Dus komt er nul uit.
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 17:11
door Rov
Buiten de torus is de B nul.
Zeker van?
Ik dacht dat
\(\oint \vec B d \vec s = 0\)
, dat wil (zoals eendavid al aangaf) niet zeggen dat
\(\vec B = 0\)
, die kringintegraal is nul omdat
\(\vec B \bot d \vec s \Leftrightarrow \vec B \cdot d \vec s = 0\)
.
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 17:42
door DePurpereWolf
De eerste formule die je hebt (in post 1) is de stroom die gaat lopen als je een geleider in de solenoid brengt. Deed heet volgens mij geen torus in het Nederlands, maar gewoon spoel. Natuurlijk is er wel een magnetisch veld,
dat kun je aan het volgende plaatje zien.
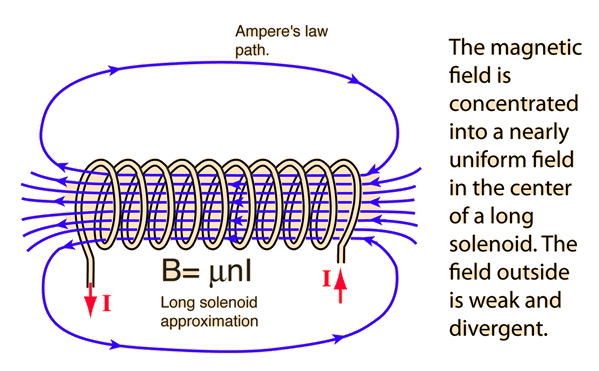
Je kunt je integraal niet zomaar overal neerzetten en dan aannemen dat de som nog moet werken.
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 17:49
door Rov
In zijn tweede post geeft hij een link naar het juist plaatje
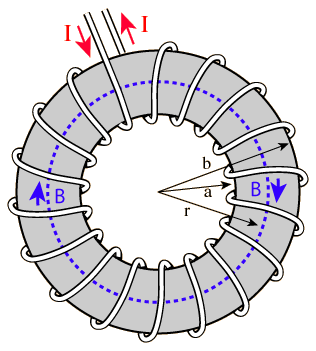
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 17:59
door DePurpereWolf
Het is nul binnen in de ring omdat de spoel afgesloten is. er is geen reden waarom er een magnetisch veld door de ring zou moeten lopen. Neem de afbeelding in mijn vorige post, en vorm de spoel aldaar om in een ringvorm, dan zie je dat er alleen magnetische veldlijnen binnen in de spoel zijn.
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 19:50
door aadkr
Alleen in de torus zelf is een magnetisch veld.
[attachment=272:scan0002.jpg]
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 20:55
door Rov
In mijn boek staat dat bij een (ideale) torus er wel degelijk een klein magnetisch veld is buiten de torus.
Re: Vraag over toepassing van de wet van amp
Geplaatst: ma 11 jun 2007, 22:42
door aadkr
Als de torus of ringkernspoel een ringkern van ferromagnetisch materiaal bevat en hij (zij) is dichtbewikkeld, dan zal het magn. veld zich binnen de torus bevinden. Het kan zijn dat er nog een zeer zwak veld buiten de torus bevindt, maar dit is te verwaarlozen.
Re: Vraag over toepassing van de wet van amp
Geplaatst: di 12 jun 2007, 10:11
door DePurpereWolf
Er zal naar mijns inziens altijd een klein magnetisch veldje rond de draden zijn. Dus in principe ook in de leegte van de torus. Deze is echter zeer klein, en niet echt belangrijk.
Re: Vraag over toepassing van de wet van amp
Geplaatst: do 14 jun 2007, 19:12
door Handsome Hermit
bedankt iedereen voor de discussie en de antwoorden.

