Een bal wordt tegen een muur geschopt met een snelheid van 20m/s onder een hoek van 40° met de horizontale. De muur staat 8,0 m ver. Hoe hoog botst de bal tegen de muur en met welke snelheid?
Ik heb van dit probleem reeds tekening gemaakt:
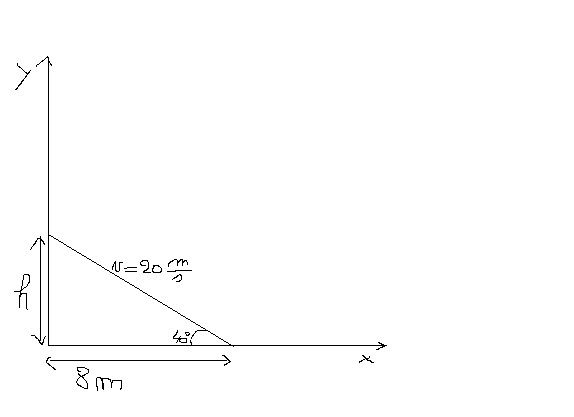
Op het eerste zicht zou ik h berekenen met: tan(40)=h/8, maar dit blijkt niet te kloppen. Iemand een idee?