Bepalen van helling van een bocht.

Malanrian

Welke helling moet een bocht met straal 150m hebben opdat een auto wrijvingsloos tegen een snelheid van 75km/h de bocht zou kunnen nemen?

Kan iemand een tip geven hoe je hieraan moet beginnen?

Jan van de Velde

Met een schets......

Verborgen inhoud

En als je het doet zoals ik levert je dat mogelijk een aftrekpunt op vanwege het gebruik van centrifugaalkrachten ipv centripetaalkrachten, maar zo voelt'ie heel logisch en kom je wel op het goeie antwoord....

Malanrian

Vooraleer ik terug kom op deze was ik al bezig met een ander vraagstuk waar ik niet wijs ui raak:

Een doos met een gewicht van 50N wordt voortgetrokken met constante snelheid door een kracht van 25N die een hoek van 50° maakt met de horizontale. Bereken de wrijvingskracht, de wrijvingscoëfficient en de normaalkracht.

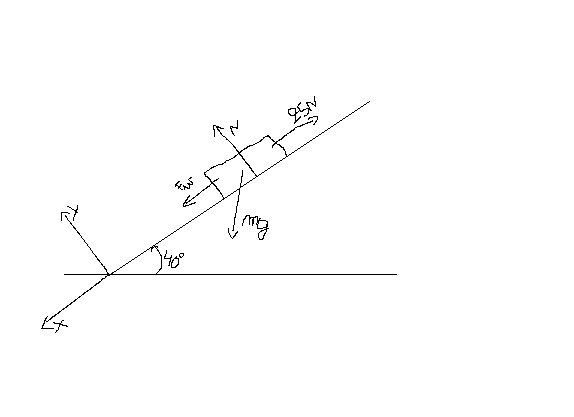
Afbeelding

Dus volgens mijn redenering:

x: mg*sin(40)+F_k-25=0

y: mg*cos(40)+N=0 => N=50cos(40) = 38,3N

Voor de normaal bekom in 38,3N, maar het zou 50N moeten zijn. Verder zou de wrijvingscoëfficient 0,38 moeten zijn en de grootte van de wrijvingskracht zou 50N moeten zijn...

Arie Bombarie

In je opgave staat 50°, terwijl je rekent met 40°, typfoutje?

Bij 50° krijg ik N = 50cos(50) = 32,1 N

En volgens mij klopt er wel meer niet, want de x component van het gewicht van de doos:

50sin(50) = 38,3 N wat al meer is dan de 25 N waar mee getrokken wordt...

Jan van de Velde

Malanrian schreef:Een doos met een gewicht van 50N wordt voortgetrokken met constante snelheid door een kracht van 25N die een hoek van 50° maakt met de horizontale. Bereken de wrijvingskracht, de wrijvingscoëfficient en de normaalkracht.

Voor de normaal bekom in 38,3N, maar het zou 50N moeten zijn. Verder zou de wrijvingscoëfficient 0,38 moeten zijn en de grootte van de wrijvingskracht zou 50N moeten zijn...

Ten eerste, pas op voor verwarring als je meerdere problemen in één topic afhandelt. We vinden het helemaal niet erg om voor twee afzonderlijke vragen twee topics te hebben

Volgens mij interpreteer je deze laatste vraag verkeerd. De doos ligt volgens mij gewoon op een horizontaal oppervlak, en wordt ze voortgetrokken door een kracht die schuin omhoog is gericht.

Een gelijkaardig probleem uit de oefenopgaven van de microcursus krachten ontbinden

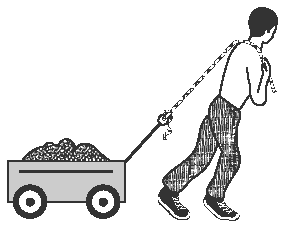
Afbeelding

(NB in die cursus vraag ik gezien het niveau alleen om de horizontale component van de trekkracht)

In Malanrian's verhaal gaat nog de verticale component ervan moeten meespelen, maar dat zie ik (gezien de antwoorden, niet gebeuren. Overigens zit er een fout in de opgave. Met een trekkracht van 25 N en een wrijvingskracht van 50 N kán die doos helemaal niet met een constante snelheid bewegen. Al helemaal niet als die trekkracht ook nog eens schuin naar boven is gericht.

Malanrian

Jan van de Velde schreef:Ten eerste, pas op voor verwarring als je meerdere problemen in één topic afhandelt. We vinden het helemaal niet erg om voor twee afzonderlijke vragen twee topics te hebben

Volgens mij interpreteer je deze laatste vraag verkeerd. De doos ligt volgens mij gewoon op een horizontaal oppervlak, en wordt ze voortgetrokken door een kracht die schuin omhoog is gericht.

Een gelijkaardig probleem uit de oefenopgaven van de microcursus krachten ontbinden

(NB in die cursus vraag ik gezien het niveau alleen om de horizontale component van de trekkracht)

In Malanrian's verhaal gaat nog de verticale component ervan moeten meespelen, maar dat zie ik (gezien de antwoorden, niet gebeuren. Overigens zit er een fout in de opgave. Met een trekkracht van 25 N en een wrijvingskracht van 50 N kán die doos helemaal niet met een constante snelheid bewegen. Al helemaal niet als die trekkracht ook nog eens schuin naar boven is gericht.

Als de doos horizontaal ligt, dan is het inderdaad wel makkelijk te berekenen! De normaal is dan gelijk aan de zwaartekracht (50N), De wrijvingskracht is dan 25cos(40)=19N, de wrijvingscoëfficient is dan 19/50=0.38.

Dank voor de hulp!

Arie Bombarie schreef:In je opgave staat 50°, terwijl je rekent met 40°, typfoutje?

Bij 50° krijg ik N = 50cos(50) = 32,1 N

En volgens mij klopt er wel meer niet, want de x component van het gewicht van de doos:

50sin(50) = 38,3 N wat al meer is dan de 25 N waar mee getrokken wordt...

Ja, typfoutje in de opgave. Het is effectief wel 40°.

Malanrian

Jan van de Velde schreef:Met een schets......

Verborgen inhoud
[attachment=989:bochthelling_arual.GIF]

En als je het doet zoals ik levert je dat mogelijk een aftrekpunt op vanwege het gebruik van centrifugaalkrachten ipv centripetaalkrachten, maar zo voelt'ie heel logisch en kom je wel op het goeie antwoord....

Dan terug naar deze...

Om de centripetaalkracht te berekenen, heb je dan geen massa nodig?

Ruben01

Om de centripetaalkracht te berekenen, heb je dan geen massa nodig?

Neen, wanneer je de evenwichtsvergelijking voor de y-componenten gaat opstellen (vgl 1) en de evenwichtsvergelijking voor de y-componenten (vgl 2) dan moet je vgl 2 eens invullen in vgl 1.

Als je correct gewerkt hebt dan zal je zien dat ja aan beide kanten van je vergelijking de massa's kan wegschrappen.

Jan van de Velde

Om de centripetaalkracht te berekenen, heb je dan geen massa nodig?

Neen, ..//.. Als je correct gewerkt hebt dan zal je zien dat ja aan beide kanten van je vergelijking de massa's kan wegschrappen.

En als je dat niet ziet is er nog een "vluchtweg". Reken het gewoon uit voor twee versschillende massa's...........

Malanrian

En als je dat niet ziet is er nog een "vluchtweg". Reken het gewoon uit voor twee versschillende massa's...........

Ik geloof dat ik het gevonden heb:

tg(a)=Fc/mg=(v²/r)/g => a=16,4°

Jan van de Velde

ik geloof het ook

Jan van de Velde

Malanrian schreef:Als de doos horizontaal ligt, dan is het inderdaad wel makkelijk te berekenen! De normaal is dan gelijk aan de zwaartekracht (50N), De wrijvingskracht is dan 25cos(40)=19N, de wrijvingscoëfficient is dan 19/50=0.38.

Dank voor de hulp!

En tóch ben ik het hier helemaal NIET mee eens. Die trekkracht heeft namelijk ook een duidelijke verticale component die bij een hoek van 40° met de horizontaal 16,07 N bedraagt.

Daardoor is de normaalkracht op de doos 50-16,07 = 33,93 N

De horizontale component van de trekkracht is 25cos(40) = 19,15 N

De doos heeft een constante snelheid, wrijvingskracht Fw is gelijk aan horizontale component van trekkracht = 19,15 N

Fw= µ x Fn

==> µ = Fw/Fn = 19,15/33,93 = 0,56.

Malanrian

Jan van de Velde schreef:En tóch ben ik het hier helemaal NIET mee eens. Die trekkracht heeft namelijk ook een duidelijke verticale component die bij een hoek van 40° met de horizontaal 16,07 N bedraagt.

Daardoor is de normaalkracht op de doos 50-16,07 = 33,93 N

De horizontale component van de trekkracht is 25cos(40) = 19,15 N

De doos heeft een constante snelheid, wrijvingskracht Fw is gelijk aan horizontale component van trekkracht = 19,15 N

Fw= µ x Fn

==> µ = Fw/Fn = 19,15/33,93 = 0,56.

Je hebt inderdaar gelijk, maar ik hou het toch maar op de oplossingen die in de cursus staan

Wetenschapsforum

Laatste berichten

Nieuwsberichten

Bepalen van helling van een bocht.

Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.

Re: Bepalen van helling van een bocht.