Hallo allemaal,
ik ben bezig met het maken van mijn praktische opdracht van wiskunde
maar ik kom er niet helemaal uit.
Ik moet van 5 dakgoten de oppervlakte van de dwarsdoorsnede berekenen.
Gegeven is dat de plaat waarvan de goten gemaakt zijn een breedte van 25 cm heeft.
Bij 2 van de goten is het mij gelukt de oppervlakte te berekenen, maar bij de andere drie loop ik vast.
Bij de bijlage heb ik gevoegd wat ik tot nu toe heb.
Ik hoop echt dat iemand mij kan helpen.
Alvast bedankt!
F.B
Laatste berichten
-
10:25
Herleiden afmetingen vanaf een foto 1
-
07:53
Rotatie van het heelal 25
-
00:49
Ervaringen met "herontdekkingen" 11
-
21:28
hall effect in vloeistof gebruiken als stromingssensor 6
-
17:59
Gezocht: de/een naam voor een getallenrij met een cauchyrij als partieelsommenrij
-
17:28
Casus uit de praktijk: positief test THC 18
-
17 apr
speciale rel. theorie 4
-
17 apr
Vreemde stank in huis 11
-
17 apr
3 vragen over mijn rooskleurige r.berekening H2netGekoppeldeHBrflowbatterij.
-
17 apr
Interpretatie reactie-energie 3
-
17 apr
Logistic equation (Pierre Verhulst,Belgian Mathematician) 5
-
16 apr
vB 9
-
15 apr
Kunnen quantum Zonnecellen 190% quantum efficiënt zijn 1
-
15 apr
Python: sockets sluiten 4
-
14 apr
Een eenvoudige logische redenering waarom tijd niet kan bestaan 'daarbuiten' 6
-
14 apr
Hoe kun je op quantumwijze getallen vinden in een rij die kleiner zijn dan getal k 3
-
13 apr
Documentenverdwijnen uit onedrive 1
-
12 apr
Behoud van impulsmoment en energie 5
-
12 apr
INLOG STORING / TIPS 4
-
09 apr
[natuurkunde] systeemgrafen 1
Nieuwsberichten
-
04 mar
Een nieuw soort magnetisme: altermagnetisme
-
31 okt
AI kan via stem diabetes vaststellen 11
-
21 okt
Einstein krijgt wéér gelijk 45
-
07 feb
witter dan wit 20
-
19 jun
irrigatie en de aardas
[Wiskunde] p.o. inhoud van een goot
Moderators: ArcherBarry, Fuzzwood
-
- Berichten: 24.578
Re: [Wiskunde] p.o. inhoud van een goot
Verplaatst naar huiswerk.
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
-
- Berichten: 177
Re: [Wiskunde] p.o. inhoud van een goot
Je kunt bij die eerste beter de schuine zijde van de driehoekjes x noemen. Dan differentieren en gelijkstellen aan 0.
-
- Berichten: 10
Re: [Wiskunde] p.o. inhoud van een goot
Maar dan kom ik er nog niet uit.
Want dan heb ik over de onderste zijde helemaal geen kennis toch?
Want dan heb ik over de onderste zijde helemaal geen kennis toch?
-
- Berichten: 177
Re: [Wiskunde] p.o. inhoud van een goot
Je moet differentieren naar x en differentieren naar alpha. Allebei dus differentieren.
dA/dx en dA/dalpha, met A = oppervlak.
De onderste zijde wordt dan 25-2x... dat rekent een stuk makkelijker dan als je de onderste zijde x noemt.
dA/dx en dA/dalpha, met A = oppervlak.
De onderste zijde wordt dan 25-2x... dat rekent een stuk makkelijker dan als je de onderste zijde x noemt.
-
- Berichten: 10
Re: [Wiskunde] p.o. inhoud van een goot
Oh dat ben ik er vergeten bij te zetten op het plaatje.
Bij het bovenste plaatje, van de trapeziumvormige goot, heb ik de onderste zijde x genoemd (de zijde EF dus).
oke, ik zal het meteen proberen!
Bij het bovenste plaatje, van de trapeziumvormige goot, heb ik de onderste zijde x genoemd (de zijde EF dus).
oke, ik zal het meteen proberen!
-
- Berichten: 10
Re: [Wiskunde] p.o. inhoud van een goot
Dan kom ik tot hier:
Omtrek=25
=2x+EF
EF=25-2x
Oppervlakte=oppervlakte BCEF+oppervlakte ABCD
=EF·AC+AB·AC
sin α=AC÷
x
AC=sin α·x
cos α=AB÷
x
AB=cos α·x
Oppervlakte=x·sin α·x+cos α·x·sin α·x
Omtrek=25
=2x+EF
EF=25-2x
Oppervlakte=oppervlakte BCEF+oppervlakte ABCD
=EF·AC+AB·AC
sin α=AC÷
x
AC=sin α·x
cos α=AB÷
x
AB=cos α·x
Oppervlakte=x·sin α·x+cos α·x·sin α·x
-
- Berichten: 10
Re: [Wiskunde] p.o. inhoud van een goot
Nee dat klopt niet
zo klopt het denk ik wel:
Omtrek=25
=2x+EF
EF=25-2x
Oppervlakte=oppervlakte BCEF+oppervlakte ABCD
=EF·AC+AB·AC
sin α=AC÷
x
AC=sin α·x
cos α=AB÷
x
AB=cos α·x
Oppervlakte=(x·sin α·x)+(cos α·x·sin α·x)
=(2x·sin α)+(2x·cos α·sin α)
Maar dan kom ik dus nog steeds niet verder.
Wie kan mij helpen?
zo klopt het denk ik wel:
Omtrek=25
=2x+EF
EF=25-2x
Oppervlakte=oppervlakte BCEF+oppervlakte ABCD
=EF·AC+AB·AC
sin α=AC÷
x
AC=sin α·x
cos α=AB÷
x
AB=cos α·x
Oppervlakte=(x·sin α·x)+(cos α·x·sin α·x)
=(2x·sin α)+(2x·cos α·sin α)
Maar dan kom ik dus nog steeds niet verder.
Wie kan mij helpen?
-
- Berichten: 177
Re: [Wiskunde] p.o. inhoud van een goot
Ik kom uit op
Hieruit
\(A = x^2 \cdot \sin{\alpha} \cos{\alpha} + (25x-2x^2)\cdot \sin {\alpha}\)
Hieruit
\(\frac {dA}{dx}\)
bepalen en dan \(\frac {dA}{d\alpha}\)
of omgekeerd -
- Berichten: 2.746
Re: [Wiskunde] p.o. inhoud van een goot
in je vraagstelling zie ik nergens iets staan wat leidt tot een extremum.
en zijn je goten symetrisch?
en algemeen is een meerdimentionaal extremumprobleem wel wat moeilijker dan wat foodanity zegt. maar hier zal het zo ook wel lukken denk ik.
en zijn je goten symetrisch?
en algemeen is een meerdimentionaal extremumprobleem wel wat moeilijker dan wat foodanity zegt. maar hier zal het zo ook wel lukken denk ik.
-
- Berichten: 177
Re: [Wiskunde] p.o. inhoud van een goot
Boven het PO van hem/haar in het word document maximale oppervlak, dus ik denk dat het om differentieren en gelijkstellen aan 0 gaat.
Ik heb trouwens ff een makkelijk overzichterlijk plaatje gemaakt:
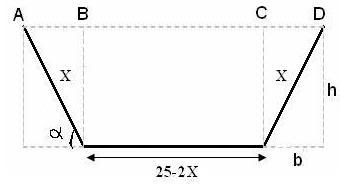
Ik heb trouwens ff een makkelijk overzichterlijk plaatje gemaakt:
-
- Berichten: 10
Re: [Wiskunde] p.o. inhoud van een goot
De goten zijn wel symetrisch.
Maar ik weet niet precies wat een extremum is, dus op die vraag kan ik geen antwoord geven.
Maar ik weet niet precies wat een extremum is, dus op die vraag kan ik geen antwoord geven.
-
- Berichten: 4.246
Re: [Wiskunde] p.o. inhoud van een goot
Een extremum is een maximum of een minimum.
Quitters never win and winners never quit.
-
- Berichten: 10
Re: [Wiskunde] p.o. inhoud van een goot
Ik zal er nog even een betere afbeelding bijvoegen vande drie goten,
want ik moest de vorige enorm verkleinen omdat het anders niet in het bericht paste.
want ik moest de vorige enorm verkleinen omdat het anders niet in het bericht paste.
-
- Berichten: 177
Re: [Wiskunde] p.o. inhoud van een goot
Dus nu leidt je even de hoogte af, met de schuine zijde genaamd x. En de base van de driehoek, oftewel AB, of CD.
Dan doe je b*h, van de twee driehoeken samen en dat plus EF (=25-2x)*h. Als het goed is komt daar mijn formule uit als A (oppervlak). Die differentieren (afgeleide bepalen) naar x en gelijk stellen aan 0 en dat doe je precies zo voor alpha.
Dan doe je b*h, van de twee driehoeken samen en dat plus EF (=25-2x)*h. Als het goed is komt daar mijn formule uit als A (oppervlak). Die differentieren (afgeleide bepalen) naar x en gelijk stellen aan 0 en dat doe je precies zo voor alpha.
