[wiskunde] inverse laplace transformatie
Moderators: ArcherBarry, Fuzzwood
- Berichten: 682
[wiskunde] inverse laplace transformatie
Goede dag,
(4s+12)/(s^2+8s+16) moet inverse Laplace worden.
Ik maak ervan:
(4s+12)/(s+4)^2
Dan breuksplitsen:
(A/(s+4))+(B/(s+4)^2)
Dan krijg ik uiteindelijk een A van 2/15 en een B van 38/15.
Dan kan ik op:
f(t) = (2/15)e^(-4t)+(38/15)te^(-4t)
Dit klopt echter niet...
Iemand een idee waar het fout gaat?
Alvast bedankt!
(4s+12)/(s^2+8s+16) moet inverse Laplace worden.
Ik maak ervan:
(4s+12)/(s+4)^2
Dan breuksplitsen:
(A/(s+4))+(B/(s+4)^2)
Dan krijg ik uiteindelijk een A van 2/15 en een B van 38/15.
Dan kan ik op:
f(t) = (2/15)e^(-4t)+(38/15)te^(-4t)
Dit klopt echter niet...
Iemand een idee waar het fout gaat?
Alvast bedankt!
Help WSF met het vouwen van eiwitten en zo ziekten als kanker en dergelijke te bestrijden in de vrije tijd van je chip:
http://www.wetenschapsforum.nl/index.ph ... opic=59270
http://www.wetenschapsforum.nl/index.ph ... opic=59270
- Berichten: 24.578
Re: [wiskunde] inverse laplace transformatie
Dat moet je nog eens nakijken, ik vind:Arie Bombarie schreef:Dan breuksplitsen:
(A/(s+4))+(B/(s+4)^2)
Dan krijg ik uiteindelijk een A van 2/15 en een B van 38/15.
\(\frac{{4s + 12}}{{s^2 + 8s + 16}} = \frac{{4s + 12}}{{\left( {s + 4} \right)^2 }} = \frac{4}{{s + 4}} - \frac{4}{{\left( {s + 4} \right)^2 }}\)
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
- Berichten: 682
Re: [wiskunde] inverse laplace transformatie
Dan staat naar alle waarschijnlijkheid hierin een fout:
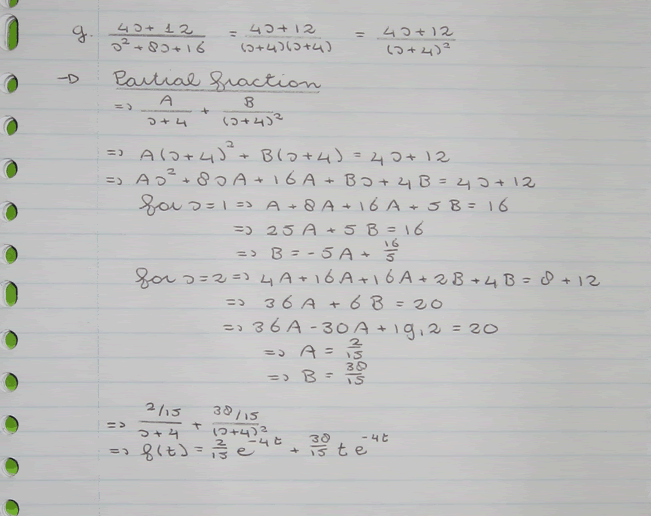
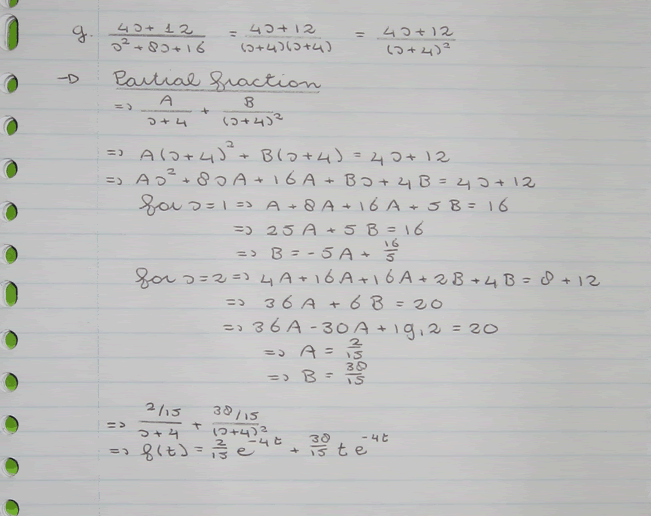
Help WSF met het vouwen van eiwitten en zo ziekten als kanker en dergelijke te bestrijden in de vrije tijd van je chip:
http://www.wetenschapsforum.nl/index.ph ... opic=59270
http://www.wetenschapsforum.nl/index.ph ... opic=59270
- Berichten: 24.578
Re: [wiskunde] inverse laplace transformatie
Het gaat vrij vroeg fout, om op noemer (s+4)² te zetten hoef je A nog maar met (s+4) te vermenigvuldigen en B met niets meer... Jij hebt kruiselings vermenigvuldigd, maar dan krijg je ook het product van de noemers en zo neem je een factor (s+4) "te veel" mee, tot noemer (s+4)³.
Je komt er dan wel uit met deze manier, maar ik geef ook even dit snelle trucje mee:
Je komt er dan wel uit met deze manier, maar ik geef ook even dit snelle trucje mee:
\(\frac{{4s + 12}}{{\left( {s + 4} \right)^2 }} = \frac{{4\left( {s + 4} \right) - 4}}{{\left( {s + 4} \right)^2 }} = \cdots = \frac{4}{{s + 4}} - \frac{4}{{\left( {s + 4} \right)^2 }}\)
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
- Berichten: 682
Re: [wiskunde] inverse laplace transformatie
Uiteraard, dank je 
Help WSF met het vouwen van eiwitten en zo ziekten als kanker en dergelijke te bestrijden in de vrije tijd van je chip:
http://www.wetenschapsforum.nl/index.ph ... opic=59270
http://www.wetenschapsforum.nl/index.ph ... opic=59270
- Berichten: 24.578
Re: [wiskunde] inverse laplace transformatie
Graag gedaan! Soms loont het de moeite om even goed te "kijken en denken" voor je de standaardmethode uit de kast haalt 
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
- Berichten: 682
Re: [wiskunde] inverse laplace transformatie
Weer een over hetzelfde onderwerp, neem aan dat ik er geen nieuw topic voor hoef te maken.
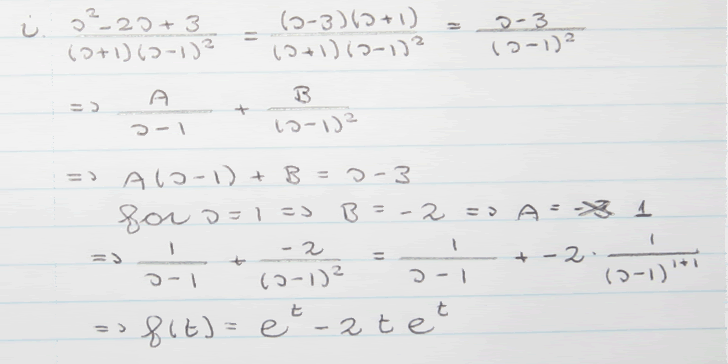
Probleem is dat het antwoord niet overeenkomt met het meegekregen antwoord...
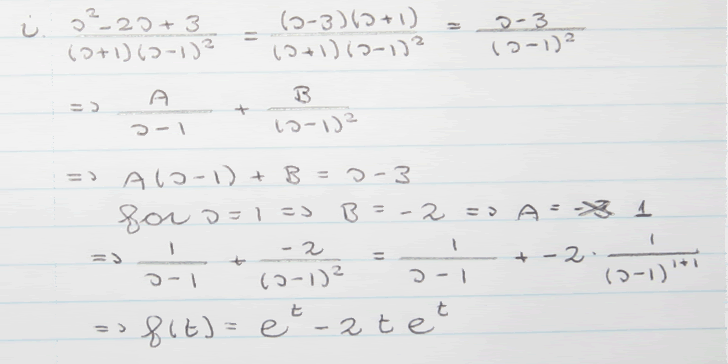
Probleem is dat het antwoord niet overeenkomt met het meegekregen antwoord...
Help WSF met het vouwen van eiwitten en zo ziekten als kanker en dergelijke te bestrijden in de vrije tijd van je chip:
http://www.wetenschapsforum.nl/index.ph ... opic=59270
http://www.wetenschapsforum.nl/index.ph ... opic=59270
-
- Berichten: 7.068
Re: [wiskunde] inverse laplace transformatie
\(\frac{s^2 - 2 s + 3}{(s+1) (s-1)^2} \neq \frac{(s - 3)(s + 1)}{(s+1) (s-1)^2}\)
- Berichten: 44
Re: [wiskunde] inverse laplace transformatie
ik merk op dat je in de tellers alleen maar constanten zet (bvb.
Dat is iets dat ik hier mis.
In het eerste geval is het 'trukje' van TD natuurlijk handiger. Voor je 2e opgave kan je het op deze manier makkelijk uitrekenen
\(\frac{A_{1}}{s+1}+\frac{A_{2}}{(s-1)^2}\)
). Ik heb altijd geleerd om, bij het splitsen in partieelbreuken, er voor te zorgen dat de graad in de teller 1 lager is dan de graad in de noemer (in dit geval: \(\frac{A_{1}}{s+1}+\frac{A_{2}s+A_{3}}{(s-1)^2}\)
.Dat is iets dat ik hier mis.
In het eerste geval is het 'trukje' van TD natuurlijk handiger. Voor je 2e opgave kan je het op deze manier makkelijk uitrekenen
- Berichten: 682
Re: [wiskunde] inverse laplace transformatie
Klopt ja, maar is volgens mij niet nodig wanneer de term in de noemer in haakjes te ontbinden is.EvilBro schreef:\(\frac{s^2 - 2 s + 3}{(s+1) (s-1)^2} \neq \frac{(s - 3)(s + 1)}{(s+1) (s-1)^2}\)). Ik heb altijd geleerd om, bij het splitsen in partieelbreuken, er voor te zorgen dat de graad in de teller 1 lager is dan de graad in de noemer (in dit geval:\(\frac{A_{1}}{s+1}+\frac{A_{2}s+A_{3}}{(s-1)^2}\).
Dat is iets dat ik hier mis.
In het eerste geval is het 'trukje' van TD natuurlijk handiger. Voor je 2e opgave kan je het op deze manier makkelijk uitrekenen
Help WSF met het vouwen van eiwitten en zo ziekten als kanker en dergelijke te bestrijden in de vrije tijd van je chip:
http://www.wetenschapsforum.nl/index.ph ... opic=59270
http://www.wetenschapsforum.nl/index.ph ... opic=59270
- Berichten: 10.179
Re: [wiskunde] inverse laplace transformatie
TD zijn truukje werkt hier nog altijd hoor  de teller ken je schrijven als: (s-1)²+2...
de teller ken je schrijven als: (s-1)²+2...
Zoek je graag naar het meest interessante wetenschapsnieuws? Wij zoeken nog een vrijwilliger voor ons nieuwspostteam.
- Berichten: 44
Re: [wiskunde] inverse laplace transformatie
@ Arie: idd, als je de teller kan ontbinden en daardoor een term uit de noemer kunt elimineren, kan er een kortere manier gebruikt worden. Maar het is altijd beter de algemene techniek te gebruiken. Dan maak je veel minder fouten en is het voor jezelf ook veel overzichtelijker omdat die methode altijd werkt. Als je begint te werken met formules die maar in bepaalde situaties geldig zijn, kan je veel makkelijker de mist in gaan.
Als ik mij niet vergis kan je ook nog dit doen:
op die manier kan je met constanten in de tellers werken
Als ik mij niet vergis kan je ook nog dit doen:
\(\frac{s^2-2s+3}{(s+1)(s-1)^2}=\frac{A}{s+1}+\frac{B}{s-1}+\frac{C}{(s-1)^2}\)
.op die manier kan je met constanten in de tellers werken
- Berichten: 682
Re: [wiskunde] inverse laplace transformatie
Op deze manier heb ik hem nu inderdaad gedaanGeoffrey schreef:@ Arie: idd, als je de teller kan ontbinden en daardoor een term uit de noemer kunt elimineren, kan er een kortere manier gebruikt worden. Maar het is altijd beter de algemene techniek te gebruiken. Dan maak je veel minder fouten en is het voor jezelf ook veel overzichtelijker omdat die methode altijd werkt. Als je begint te werken met formules die maar in bepaalde situaties geldig zijn, kan je veel makkelijker de mist in gaan.
Als ik mij niet vergis kan je ook nog dit doen:\(\frac{s^2-2s+3}{(s+1)(s-1)^2}=\frac{A}{s+1}+\frac{B}{s-1}+\frac{C}{(s-1)^2}\).
op die manier kan je met constanten in de tellers werken
Help WSF met het vouwen van eiwitten en zo ziekten als kanker en dergelijke te bestrijden in de vrije tijd van je chip:
http://www.wetenschapsforum.nl/index.ph ... opic=59270
http://www.wetenschapsforum.nl/index.ph ... opic=59270
- Berichten: 24.578
Re: [wiskunde] inverse laplace transformatie
Nee, die fout wordt veel gemaakt. Je moet pas een lineaire teller voorstellen als de noemer van de vorm p(x)n is met p(x) van de tweede graad en negatieve discriminant. Voor q(x)n met q(x) lineair, volstaat steeds een constante teller.Geoffrey schreef:Ik heb altijd geleerd om, bij het splitsen in partieelbreuken, er voor te zorgen dat de graad in de teller 1 lager is dan de graad in de noemer (in dit geval:\(\frac{A_{1}}{s+1}+\frac{A_{2}s+A_{3}}{(s-1)^2}\).
Dat is iets dat ik hier mis.
"Malgré moi, l'infini me tourmente." (Alfred de Musset)