Moderators: dirkwb , Xilvo
Forumregels
(Middelbare) school-achtige vragen naar het forum "Huiswerk en Practica" a.u.b.
Zie eerst de
Huiswerkbijsluiter
Berichten: 203
Wat ik heb begrepen van anderen is dat zelfs de verzameling elementen van \(\rr\)
op het interval
\(\langle 0,1 \rangle\)
overaftelbaar is.
Met andere woorden: Je kunt niet alle elementen/waarden binnen dat interval afbeelden op een element van
\(\nn\)
.[/color]
Of nog anders gezegd: je kunt niet alle elementen 'tellen'.
Verbeter me alsjeblieft hier al als ik dit fout heb; ik ben pas sinds deze avond 'bekend' met het begrip (over)aftelbaarheid en kardinaliteit.
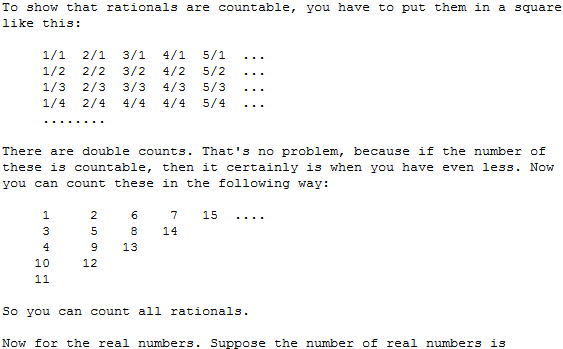
Via Google vond ik een mooie en duidelijke uitleg van "Dr. Math" over waarom alle waarden van de verzameling \(\qq\)
te tellen zijn: aftelbaar zijn. Zie hier:[/color]
Bron: http://mathforum.org/library/drmath/view/52830.html http://mathforum.org/library/drmath/view/52830.html \(\qq\)
te kunnen noteren, om vervolgens te kunnen zeggen dat het evenveel elementen bevat als
\(\nn\)
...
Waarom geldt dat dan niet, als je alle elementen van
\(\rr\)
binnen het interval
\(\langle 0,1 \rangle\)
op een overzichtelijke manier noteert?[/color]
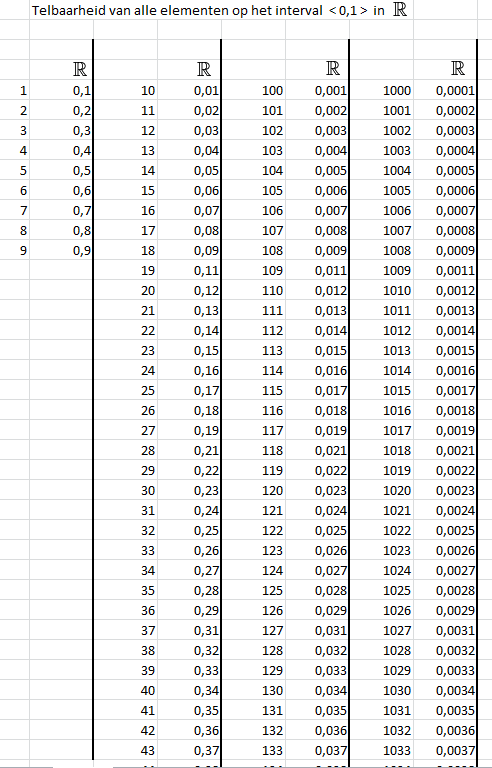
Want, ja... Ik vind dat als jullie me maar genoeg tijd geven, ik álle elementen daarvan kan noteren.
Dus ik stel: De verzameling van \(x \epsilon \rr \)
|
\(0<x<1\)
bevat evenveel elementen als
\(\nn\)
(zo noteer je dat toch?)[/color]
Mijn vraag aan jullie:
Hieronder mijn beginnetje aan het noteren van al die elementen:
dus.
Berichten: 203
Excuses voor de dubbelpost, maar bewerken gaat niet zo lekker.
dus.
Berichten: 10.179
Als ik je juist begrijp, gaat het je erover dat de reële getallen aftelbaar zouden zijn. Bestudeer dan eerst eens het
diagonaalargument van Cantor . Andere bewijzen zijn ook mogelijk, maar ik vind dit een van de inzichtelijkste...
Berichten: 2.097
En om aan te tonen dat jouw huidige lijstje niet volledig is:
"Why must you speak when you have nothing to say?" -Hornblower
Berichten: 203
Och, natuurlijk. Stom dat ik niet aan die getallen heb gedacht. Die kun je natuurlijk nooit decimaal schrijven, of állemaal in een rijtje zetten.
dus.
Berichten: 10.179
Het niet decimaal kunnen schrijven is nog niet eens je grootste probleem. Immers zijn de rationale getallen wél aftelbaar. En die bevatten ook getallen als 1/3...
Pluimdrager
Berichten: 10.058
Decimaal geschreven is er wel een principieel verschil tussen bv 1/7 en pi/4.
Berichten: 5.679
Zelfs de algebraïsche getallen zijn aftelbaar. Dit zijn alle getallen die het nulpunt zijn van een veelterm.
Daaronder vallen - behalve alle rationale getallen - dus ook irrationale getallen zoals
\(\sqrt{2}\)
of
\(\frac{\sqrt[7]{20}}{8+\sqrt[3]{5}}\)
.
In theory, there's no difference between theory and practice. In practice, there is.