Hierbij gebruikte hij de volgende formule:
Grondtal e
- Berichten: 2.005
Grondtal e
Leonhard Euler heeft het grondtal
Hierbij gebruikte hij de volgende formule:
\(e\)
ingevoerd.Hierbij gebruikte hij de volgende formule:
\(e=1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\frac{1}{5!}+etc\)
Wat ik me afvraag, hoe is hij ooit op het idee gekomen om deze getallen te gebruiken? Op Wikipedia kan ik ook niet echt een antwoord vinden, of kijk ik er overheen?...verhit de dichloormono-oxide tot 277 graden Celcius en geniet van het effect...
- Berichten: 24.578
Re: Grondtal e
De letter 'e' komt in elk geval van Euler, maar ben je zeker dat hij dit getal zo gedefinieerd heeft?
Er zijn andere definities mogelijk en volgens mathworld was Newton de eerste die deze reeks gebruikte als definitie (in een publicatie).
Heb je op de Nederlandstalige wiki gekeken? Op de Engelse wiki staat een stukje over de geschiedenis.
Er zijn andere definities mogelijk en volgens mathworld was Newton de eerste die deze reeks gebruikte als definitie (in een publicatie).
Heb je op de Nederlandstalige wiki gekeken? Op de Engelse wiki staat een stukje over de geschiedenis.
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
- Berichten: 2.005
Re: Grondtal e
Dat was inderdaad de Nederlandse Wiki waar ik heb gekeken.
Alleen bij de historie staat o.a. dit:
Alleen bij de historie staat o.a. dit:
\(\lim_{\nrightarrow\inf}\left(1+\frac{1}{n}\right)^n\)
Alleen limieten heb ik nog niet gehad bij wiskunde, dus dit zegt mij niet zo heel veel ben ik bang......verhit de dichloormono-oxide tot 277 graden Celcius en geniet van het effect...
- Berichten: 24.578
Re: Grondtal e
Dat is een andere definitie. Je hebt limieten misschien nog niet echt behandeld, maar die andere definitie (de oneindige som) is in feite ook een limiet 
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
- Berichten: 2.005
Re: Grondtal e
Dit is de andere definitie:
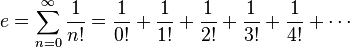
Ik ben alleen bang dat we de dingen boven, onder en naast het somteken ook nog niet hebben gehad. Ik weet wel dat de scheve 8 staat voor oneindig, maar waarom alles zo staat enzo, zegt mij compleet niks
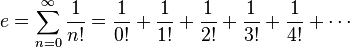
Ik ben alleen bang dat we de dingen boven, onder en naast het somteken ook nog niet hebben gehad. Ik weet wel dat de scheve 8 staat voor oneindig, maar waarom alles zo staat enzo, zegt mij compleet niks
...verhit de dichloormono-oxide tot 277 graden Celcius en geniet van het effect...
- Berichten: 314
Re: Grondtal e
Die sigma is een sommatieteken. n is een variabele waarde die gaat van 0 tot oneindig (natuurlijke getallen). Telkens moet je die n-waarde invullen in de uitdrukking die na het sommatieteken komt en zo bekom je alle termen van de som.
- Berichten: 24.578
Re: Grondtal e
Voor uitleg over die notatie voor een som, zie ook hier.
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
-
- Berichten: 137
Re: Grondtal e
Hier staat eigenlijk het getal 'n' bij de 0 begint en je oneindig lang door moet tellen. Het vertelt ook dat je bij elke 'n' die je hebt het door 1 moet delen. Nog iets belangrijks: misschien denk je dat 1/0! niet klopt omdat je niet door 0 kunt delen, maar 0! = 1. Ik hoop dat je het nu begrijpt.PdeJongh schreef:Dit is de andere definitie:
Ik ben alleen bang dat we de dingen boven, onder en naast het somteken ook nog niet hebben gehad. Ik weet wel dat de scheve 8 staat voor oneindig, maar waarom alles zo staat enzo, zegt mij compleet niks
PS: als ik iets fout vertel wil iemand me dan aub corrigeren?
- Berichten: 24.578
Re: Grondtal e
Wat bedoel je met telkens door 1 delen? Je moet voor elke n, 1/n! doen en optellen...Isaac Newton schreef:Het vertelt ook dat je bij elke 'n' die je hebt het door 1 moet delen.
(...)
PS: als ik iets fout vertel wil iemand me dan aub corrigeren?
"Malgré moi, l'infini me tourmente." (Alfred de Musset)
-
- Berichten: 137
Re: Grondtal e
Dat was ik vergeten erbij te zetten. Sorry. Dat optellen is logisch, omdat het een som is. Daarom schreef ik dát niet op.
- Berichten: 2.005
Re: Grondtal e
Ik snap nu in ieder geval de berekening. Dat is al iets 
Dan snap ik die pagina op wikipedia waarschijnlijk ook beter, en kom ik er hopelijk achter hoe Euler op het idee is gekomen om deze berekening te maken
Dan snap ik die pagina op wikipedia waarschijnlijk ook beter, en kom ik er hopelijk achter hoe Euler op het idee is gekomen om deze berekening te maken
...verhit de dichloormono-oxide tot 277 graden Celcius en geniet van het effect...
- Pluimdrager
- Berichten: 6.591
Re: Grondtal e
Het binomium van Newton
Dus:
\((a+b)^n=a^n+\left(n boven 1\right) a^{(n-1)}b + \left( n boven 2\right) a^{(n-2)} b^2+ ...... +b^n\)
\((a+b)^n=a^n+\frac{n}{1!}a^{(n-1)}b+\frac{n(n-1)}{2!} a^{(n-2)} b^2+.....+ 1 b^n\)
Voor n nadert naar oneindig geldt dan:\((1+b)^n=1+\frac{n}{1!}b+\frac{n(n-1)}{2!} b^2 + . ....\)
\((1+\frac{1}{n})^n=1+\frac{n}{1!}\frac{1}{n}+\frac{n(n-1)}{2!}\frac{1}{n^2}+.....\)
\((1+\frac{1}{n})^n=1+1+\frac{1}{2!}\frac{n}{n}\frac{(n-1)}{n} +\frac{1}{3!}\frac{n}{n}\frac{(n-1)}{n}\frac{(n-2)}{n} + .......\)
Als n nadert tot oneindig , dan worden de termen:\(\frac{n-1}{n} \frac{n-2}{n}\)
enzovoort gelijk aan 1Dus:
\(Lim_{\nrightarrow one\indig}(1+\frac{1}{n})^n=1+1+\frac{1}{2!}+\frac{1}{3!}+.....\)
-
- Berichten: 251
Re: Grondtal e
De definitie van limiet is in feite eenvoudiger dan die van oneindige som. De limiet zegt wat er met de termen gebeurt als variabele erg, heel erg, groot (en nog groter dan dat) wordt.PdeJongh schreef:Dat was inderdaad de Nederlandse Wiki waar ik heb gekeken.
Alleen bij de historie staat o.a. dit:\(\lim_{\nrightarrow\inf}\left(1+\frac{1}{n}\right)^n\)Alleen limieten heb ik nog niet gehad bij wiskunde, dus dit zegt mij niet zo heel veel ben ik bang...
Je hoeft dus alleen op die enkele 'laatste' uitdrukking te letten. In tegenstelling tot de som, waar je ook nog alle voorgaande termen erbij moet optellen.
(wiskundigen poepen mij uit voor de volgende regel, maar het maakt het idee duidelijk):
\(\lim_{\nrightarrow\inf}\left(1+\frac{1}{n}\right)^n = (1+\frac{1}{\veel})^{\veel}\)
-
- Berichten: 718
Re: Grondtal e
Ik betwijfel of precies bekend is hoe Euler tot zijn definitie kwam, want de meeste artikelen over (om het even welke) wiskundige ontdekking geven alleen maar een deductieve afleidingen en maar zelden een verslag van de veel interessantere ontdekkingsreis die tot deze ontdekking heeft geleid, maar het zou zo gegaan kunnen zijn:PdeJongh schreef:Ik snap nu in ieder geval de berekening. Dat is al iets
Dan snap ik die pagina op wikipedia waarschijnlijk ook beter, en kom ik er hopelijk achter hoe Euler op het idee is gekomen om deze berekening te maken
Differentiaalrekening was nog redelijk nieuw en het ligt voor de hand om te kijken of je een functie f(x) kunt vinden met de eigenschap dat hij f'(x)=f(x). Nu is vrij gemakkelijk af te leiden dat dat iets van de vorm Bax moet zijn omdat dat als afgeleide BCax heeft waarbij de constante C wordt bepaald door de keuze van a. Niet zo gemakkelijk is af te leiden wat je voor a moet kiezen om te zorgen dat C=1.
Euler hield zich ook veel met reeksen bezig en zal waarschijnlijk al snel gezien hebben dat voor de functie g(x) met:
\(g(x)=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+\frac{x^5}{5!}+etc\)
geldt dat g'(x)=g(x) (dat is eenvoudig in te zien, probeer maar).Afgezien van de (niet belangrijke) constante B is dit de gezochte exponentiële functie f(x) die daarmee ook nog een definitie voor e oplevert door x=1 te kiezen.
Re: Grondtal e
Een gezonde manier om het getal e te introduceren (zonder limieten) is als volgt:PdeJongh schreef:Dat was inderdaad de Nederlandse Wiki waar ik heb gekeken.
Alleen bij de historie staat o.a. dit:\(\lim_{\nrightarrow\inf}\left(1+\frac{1}{n}\right)^n\)Alleen limieten heb ik nog niet gehad bij wiskunde, dus dit zegt mij niet zo heel veel ben ik bang...
Teken de grafiek van y = 1/x en de 2 vertikale lijnen x=1 en x=a. Zie tekening.

De oppervlakte van het blauwe gebied is 1 als de rechter vertikale lijn ligt bij x=e !!!
Dit is de manier waarop in sommige leerboeken het getal e wordt vastgelegd.
De oplossing van
\(3^x=7\)
wordt geschreven als \(x =^3\log(7)\)
en in het algemeen: De oplossing van \(a^x=b\)
wordt geschreven als \(x =^a\log(b)\)
Je kunt met bovenstaande definitie van e aantonen dat,als je de grafiek van y=1/x spiegelt in de lijn y=x dan ontstaat de grafiek met vergelijking
\(y =^e\log(x)\)
Het getal 2,7182818... dook zo vaak op dat men voor dat getal een aparte letter heeft bedacht, de letter e.Het getal e duikt b.v. op in de volgende situaties:
1.) Houdt een touwtje aan de uiteinden vast. In de vergelijking van de grafiek van het touwtje duikt de letter e op.
2.) Formule voor de continue rentebijschrijving in de bankwereld.
3.) Definitie voor sinus en cosinus (voor gevorderden).
4.) Radioactief verval; groeisnelheid van bacterien.
5.) en hier op het forum