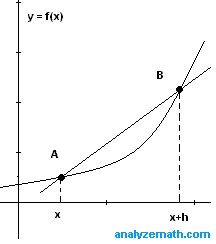
een kleine vraag over differentieerbaarheid. Stel ik heb een functie
Betekent dat, dat ik ook bijv. de functie
Bedankt voor het beantwoorden van mn vragen.
Moderators: ArcherBarry, Fuzzwood
Vreemd dat jullie afgeleiden voor limieten zien - hoe is de afgeleide in jouw cursus dan gedefinieerd?Hallo, het is meer op basis van universiteit. Ik zie namelijk vragen van hoofdstuk 5 al vragen over afleidbaarheid, dus gaf dat een aanleiding voor mij om te denken dat je het ook kon uitleggen zonder limieten. (Hoofdstuk 6 is limieten...)
Waarom maak je geen grafiek van deze functie, dan moet je het eigenlijk direct 'zien'.ntstudent schreef:Hallo,
een kleine vraag over differentieerbaarheid. Stel ik heb een functie\(y(x) = |x|\), dan is deze functie nie afleidbaar in punt x=0. Maar ik snap niet zo goed wat de definitie is van afleidbaarheid.