Pagina 1 van 1
cot
Geplaatst: vr 24 nov 2023, 14:50
door ukster
ΔDEF , G ligt op EF, ∠DGF= θ
te bewijzen: EFcotθ=GFcotE - EGcotF
Re: cot
Geplaatst: vr 24 nov 2023, 15:18
door sensor
Klopt dit?
- In \( \Delta DGF \): \( \cot(\theta) = \frac{DG}{GF} \), dus \( DG = GF \cot(\theta) \).
- In \( \Delta DGE \): \( \cot(E) = \frac{DE}{EG} \), dus \( DE = EG \cot(E) \).
- In \( \Delta DGF \): \( \cot(F) = \frac{DF}{FG} \), dus \( DF = GF \cot(F) \).
Re: cot
Geplaatst: vr 24 nov 2023, 16:34
door ukster
Ik denk van niet!
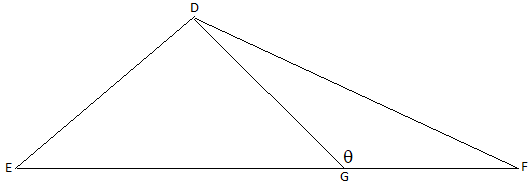
- driehoek.png (2.62 KiB) 3202 keer bekeken
Re: cot
Geplaatst: wo 29 nov 2023, 13:49
door ukster